正方体的表面积公式 正方形的表面积
前段时间有人问,球的体积计算公式是什么?
由于长期依赖各类搜索,再加上对睡觉,刷剧,电子竞技等一系列新兴趣的开发,这些似曾相识的公式早被我抛诸脑后。之后再拿起笔尝试推导我才愕然发现,基础的微积分计算法则好像也有些生疏了。
于是我开始了相关探索,半天下来,不仅成功算了个球的表面积,还算了个球的体积,而这个过程,和微积分法则毫无关系。那么怎样不用微积分就能算个球呢?
首先,抛弃了微积分这一曲线计算利器,我们的替代工具是:一点点相似三角形知识,一点点空间想象力,再加上中国古代数学家智慧的结晶——祖暅原理。
算个球的表面积!
众所周知,球的表面积公式是 4πr2,正好是同半径圆形面积的4倍,这不禁让人浮想联翩,为什么正好是 4 倍呢?难道圆形面积和球体面积之间有什么不可告人的秘密?顺着这个思路下去你可能会觉得完全无从下手,感到弱小,可怜,又无助。
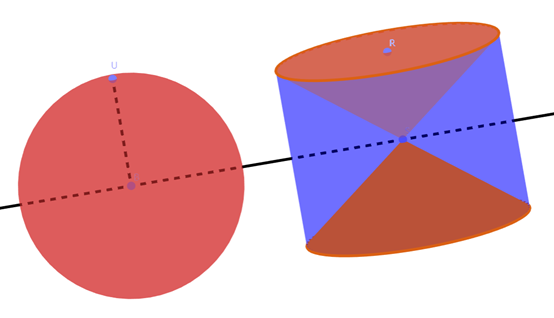
这也正是我初期经历的心路历程,直到我发现了另一个秘密:4πr2正好是这个球外接圆柱的外围面积。
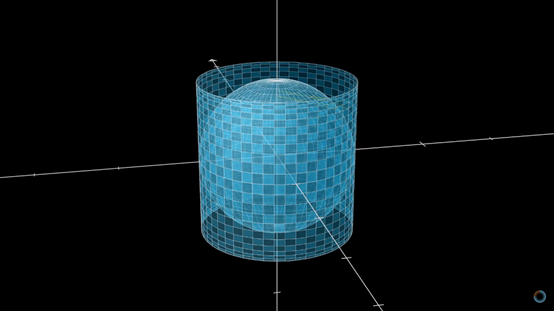
想象一下,如果把球表面划分小块,沿水平向四周投影,按理来说,这样投出的小块就可以正好铺满外面这个”圆筒”。因为圆筒的面积是圆周长乘上筒高:2πr*2r = 4πr2,和里面这颗球的表面积不谋而合!
就像下图右上角示意的那样,球上的小块被投影到圆筒上会变形,它们的宽度可能增大,而高度会相应变小。
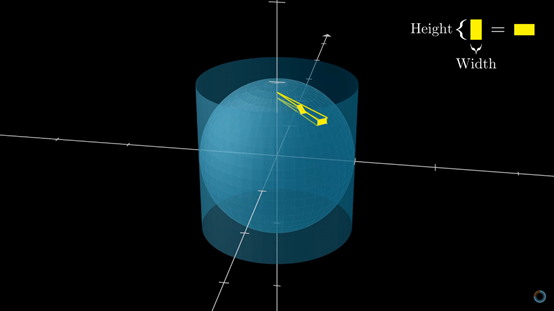
小块可以从平视和俯视两个方向来观察。那我们就来看看,投影过程中,我们的小块到底经历了什么不为人知的变化。
先看俯视图:
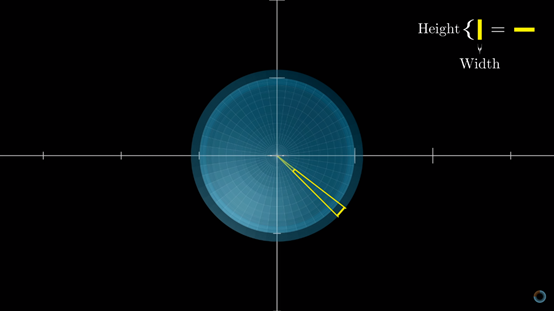
从中心轴往外投影,聪明的你一定已经发现,投影的距离越远,小块就会变得越宽。
所以纬度越高的地方,也就是越靠近上下顶点的小块,投到圆筒上之后,宽度增加得越多;位于赤道上的小块与圆筒相接,宽度也就不发生变化。
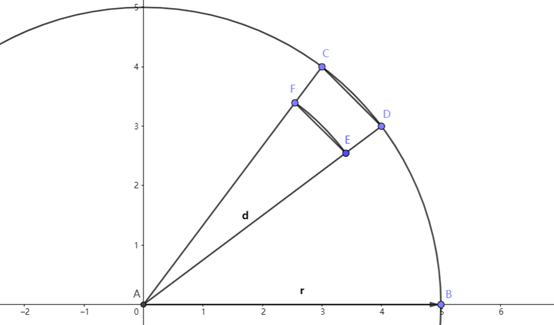
如果你知道相似三角形的比例关系,由于 △AEF和△ADC 相似,所以,这个增大的倍数是 r/d,也就是
CD/EF = r/d
对于球上不同的纬度,d 会改变,而球的半径 r 不变。越靠近两极,d 越小,r/d 就越大,小块的宽度增加也就越多,这和我们观察到的现象一致。
类似地,可以看看平视方向的情况:
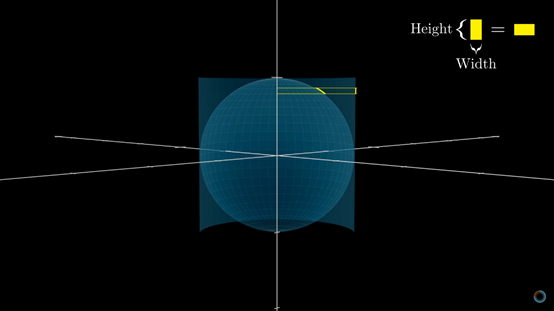
显然,这个方向上的投影会让小块的高度萎缩,也就是黄色的线段长度会缩短。
因为球的体态圆胖,越靠近两极,小块越是趋近“平躺”,投影之后高度萎缩的也越多;而在赤道上,小块直立,投影不改变小块的高度。
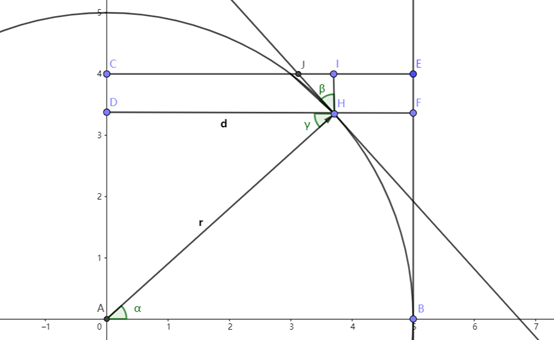
显然 ∠α=∠β=∠γ,于是 △HAD,△HIJ 两个三角形是相似三角形,根据比例关系,我们知道:
EF/JH = d/r
也就是说,平视方向投影会让小块高度萎缩,缩小比例是 d/r。
于是神奇的现象发生了,球上的每一个小块经过投影之后形状的确会发生变化,宽度拉长了 r/d 倍,同时高度萎缩了 d/r 倍,而这两个倍数相乘正好等于 1。
如此一来,小块投影前后的面积其实没有变化!仅仅利用几个三角形,我们就开心的证明了:计算球的面积可以用外接圆筒的面积来替代。
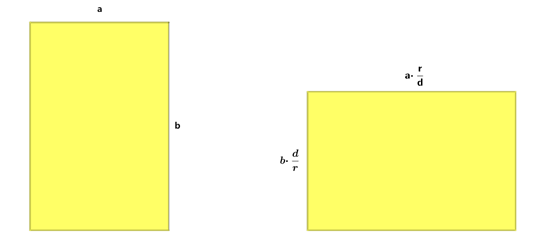
那么,算个球的表面积 S球= S筒 = 2πr*2r = 4πr2。
祖暅原理
祖暅原理又叫 Cavalieri’s Principle(卡瓦列里原理),因为卡瓦列里在17世纪提出了类似的等积原理,用于复杂几何领域,但实际上祖暅的发现比他早了1100年。
“幂势既同,则积不容异”这句话就出自于祖暅。如果你对高中数学课本有印象,也许记得这里的“幂”指体积,“势”则为高度。意思就是:高度相同的物体,如果每个剖面面积也一样,它们的体积就相等。
祖暅原理的提出本是为了解决计算牟合方盖的体积问题,从而算球的体积。但现在更加常见的用法是下面这样:
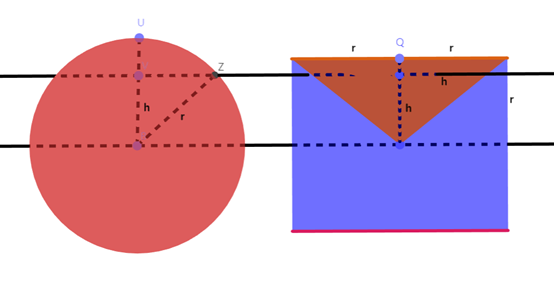
于是,算个球问题一下变成了算圆柱和圆锥的体积问题。
算个球的体积!
了解了祖暅原理,我们就可以绕过微积分,直接算球了!
由祖暅原理,半球的体积经过我们巧妙的转化,成了用圆柱和圆锥的体积来表示。
众所周知,圆柱体积是圆面积和高度相乘,V圆柱= πr2*r = πr3。而圆锥的体积,假如你不知道,查阅资料会发现 V圆锥= πr3/3,正好是圆柱的三分之一。
好奇宝宝也许会问,三分之一是怎么来的?既然你诚心诚意的问了,祖暅会大发慈悲的为你解答。
我们还是逮住之前的那个圆锥(截面面积是πh2),然后把烦人的 π 除去,截面积就成了 h2。那么谁的截面积是用 h2 表示呢?答:边长和高度都是 r 的四棱锥。
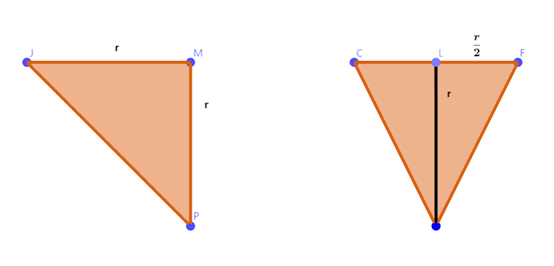
这下好了,仅仅是做了个除法,问题似乎已经简单多了!
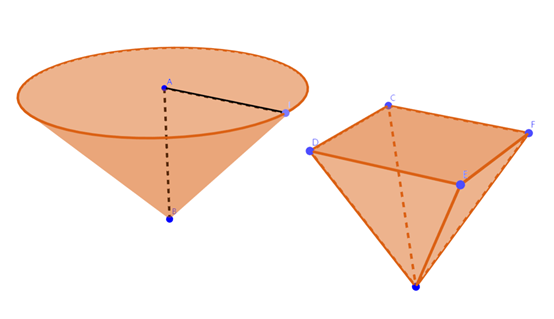
但你可能还是会问,四棱锥的体积又要怎么计算呢?别着急,我们先好好观察一下这个四棱锥。它的顶点在中心上方,感觉还是不够友好,怎么能再变换一下形状呢,没错,是时候祭出祖暅原理了。
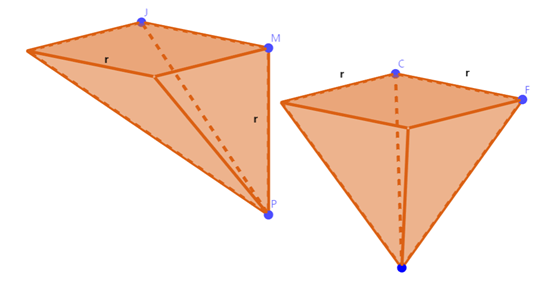
到了这里,问题基本上已经解决了。什么,你还没看出来?调动你的空间想象力,调整一下角度,把这样的四棱锥放在正方体里似乎正合适,你能看出可以同时放进几个吗?
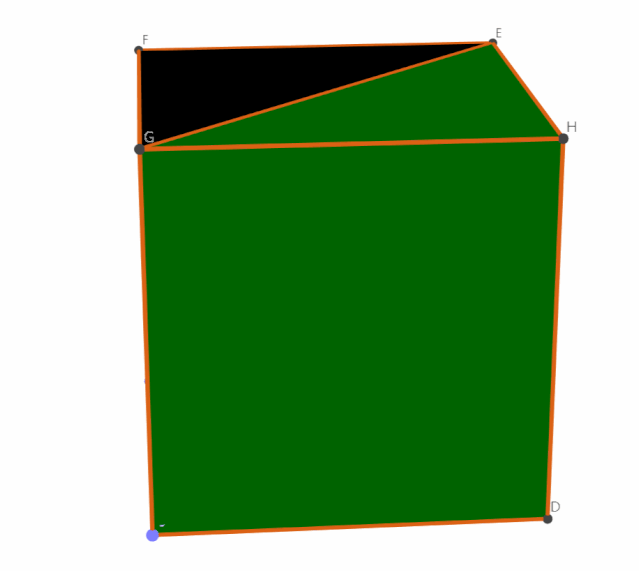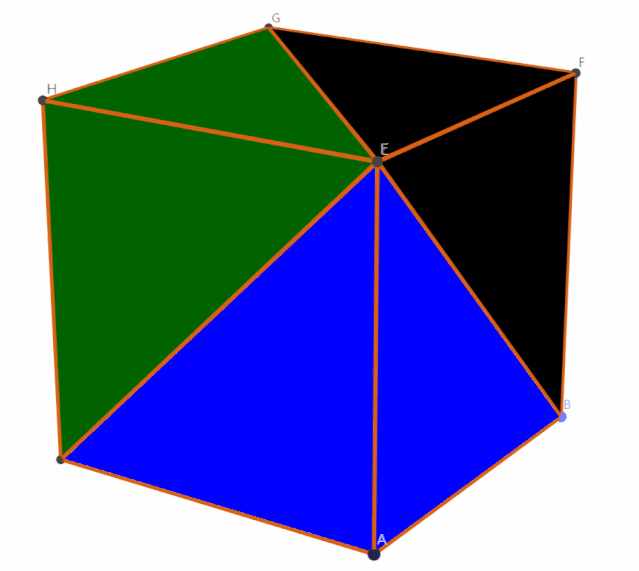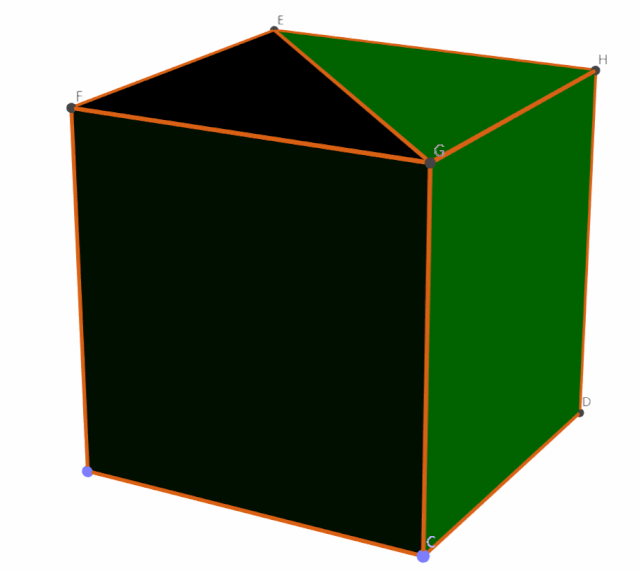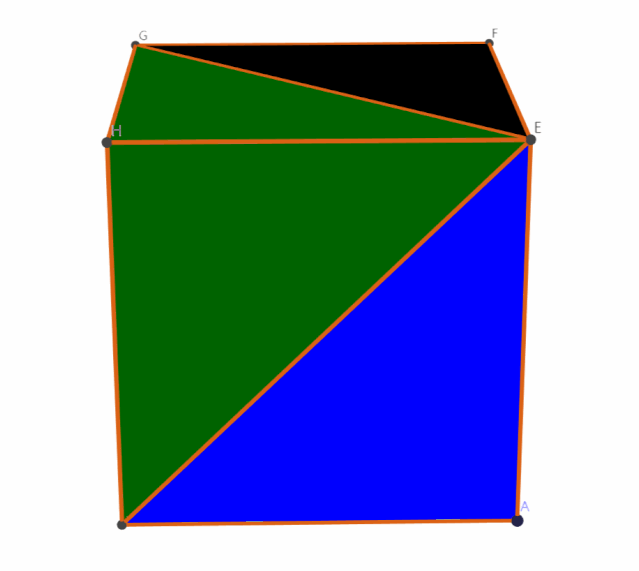
是 3 个!万事大吉?
正方体的体积显然是 r3,这样一来,四棱锥体积就是 r3/3。接着,对应圆锥的体积只需要乘上 π,V圆锥= r3/3*π。最后半球的体积 V半球= V圆柱 - V圆锥= πr3-πr3/3 = 2/3 (πr3),所以 V球= 4/3 (πr3),是不是和书上写的公式一模一样呢!
成功算球!完结撒花?
作为一期数学类的硬核推送,小编想说的是,很多时候只要切换一下思路,尝试别的工具,就可能开辟出新的道路。
所谓的数学之光,我想也就是在这里。
参考资料
Ⅰ. http://youtu.be/4_BEpekImQg
Ⅱ. http://b23.tv/av33120854
来源:牛油果进化论
编辑:Quanta Yuan
↓ 点击标题即可查看 ↓
1. 如果太阳biu的一声熄灭了,地球上会发生什么事情?
2. 每个摊煎饼的大妈,都是隐藏的流体力学专家
3. 你看的是《长安十二时辰》,我看的却是一部黑科技科普剧
4. 数学的深渊
5. 掉入海底一万米
6. 别人用脚、用声波都能打开瓶盖,为啥有的女生却拧不开?
7. 这是一篇理工男写的口红科普文
8. 声音最大能有多大?
9. 盲人看到的世界真是黑漆漆一片吗?
10. 用过的吸管不要扔,在火上烤一下,隔壁的小孩都...
A股市场:看着简单却很关键的基础知识
做任何事情都要先打好根基才能更加的稳固,走的更远。炒股同样需要先打好根基。对一些市场的基本知识还是要有一定的了解,才能更好的在市场里冲锋。这些看着简单,一看就会的东西平时可能没有用,但是说不定那个时候就是救命的稻草。今天分享给大家,希望对你有所帮助。大财经2023-11-29 14:37:490000合景泰富5月预售金额锐减超4成 短债规模超200亿推进境外债务重组
长江商报奔腾新闻记者江楚雅5月楼市降温明显,房企销售也出现下跌。6月5日,合景泰富(01813.HK)披露2023年5月销售简报。公告显示,2023年5月合景泰富预售金额23.8亿元,较去年同期减少42.2%;预售建筑面积14.9万平方米,较去年同期减少24.7%。0000魏桥创业集团:推进本地化进程 印尼籍员工与企业共同成长
【共建“一带一路”倡议十周年·魏桥实践】推进本地化进程印尼籍员工与企业共同成长魏桥创业集团致力于把宏发韦立氧化铝公司办成印尼本土化公司。大财经2023-10-12 14:19:500002一天吃透一家上市公司:万华化学
#万华化学#本报告主要介绍了万华化学的业务结构和战略布局,包括其在MDI主业、石化产业平台和专用化学品领域的发展。万华化学是一家全球化运营的综合性化工企业,拥有310万吨的MDI产能居世界第一,并积极向下游布局高附加值的专用化学品,打造综合性化学品公司。更多重要内容、核心观点,请参考报告原文。1.公司概况大财经2023-11-15 14:11:090000轶峰新材2022年净利1010.65万同比增长157.78% 营业收入增加
挖贝网4月22日,轶峰新材(839754)近日发布2022年年度报告,报告期内公司实现营业收入50,690,145.60元,同比增长10.26%;归属于挂牌公司股东的净利润10,106,547.89元,同比增长157.78%。报告期内经营活动产生的现金流量净额24,506,429.13元,归属于挂牌公司股东的净资产39,057,676.64元。0000




