自由落体公式 自由落体加速度公式
搜索群星10月榜
自由落体运动,物体仅受重力的作用,沿着竖直线下落。
早在万历年间(1572-1620),伽利略就通过比萨斜塔实验,发现了自由落体定律。
1685年,牛顿在“自然哲学的数学原理”中,提出了牛顿三大定律。
根据牛顿第二定律,mg = ma,自由落体加速度 = 重力加速度g。
(自由落体加速度表达的是惯性,重力加速度表达的是引力)
自由落体运动的速度 v = gt,位移 s = 1/2 gt^2.
如果下落的起点与终点之间的高度差为y的话,那么所需要的时间 t = (2y/g)^0.5。
起点与终点在一条竖直线上,不需要微积分,只用简单的二次代数方程就可以算出来。
但是,如果起点和终点不在一条竖直线上,这个问题就会变得很复杂,甚至在1696年被伯努利拿来考验牛顿
这就是最速降线问题。
1,最速降线问题,
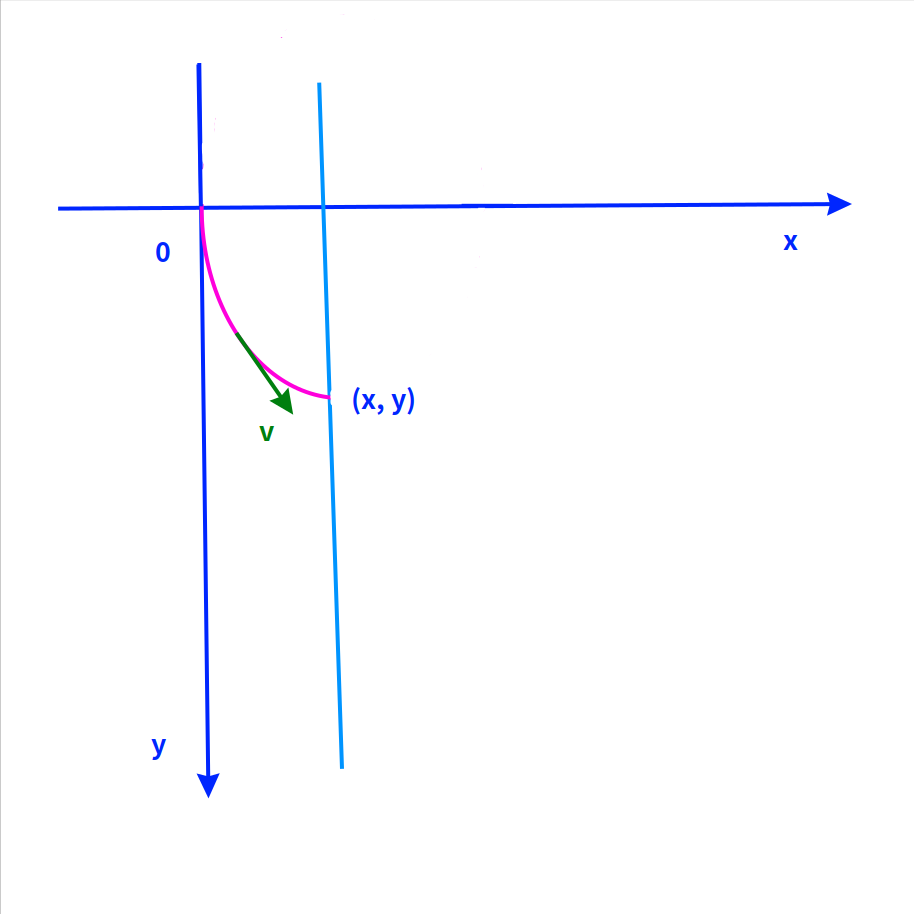
如图,不管在不在一条竖直线上,根据能量守恒定律,速度的值都是 v = (2gy)^0.5。
速率与x坐标是没关系的,因为重力做功只和高度差有关,与路径无关。
只是不在一条竖直线上时,速度的方向是变化的。
但不在一条竖直线上时,曲线的切线方向也是变化的。
并且,速度的方向始终沿着曲线的切线方向,所以它依然是个均匀加速的问题。
只是这么稍微一偏之后,就得使用微积分了:
而且,就算使用了微积分之后,问题依然不好解决。
两点之间的直线只有一条,但两点之间的曲线有无数条。
到底哪一条曲线是最节省时间的?
2,反证法、微扰论,
首先,最节省时间的曲线一定是光滑的,不可能是波纹状的。
因为,在非常微小的间隔内,速度可以认为是近似不变的,而波纹状曲线比光滑曲线具有更大的弧长。
显然,ds = vdt,波纹状的ds更大,所以肯定更费时间。
所以,最速降线的一阶导数肯定是连续变化的,而且一阶导数不能有极值点,也就是说二阶导数不能有零点。
否则,就成了波纹线了:只要把它稍微取直,花费的时间就会减少。
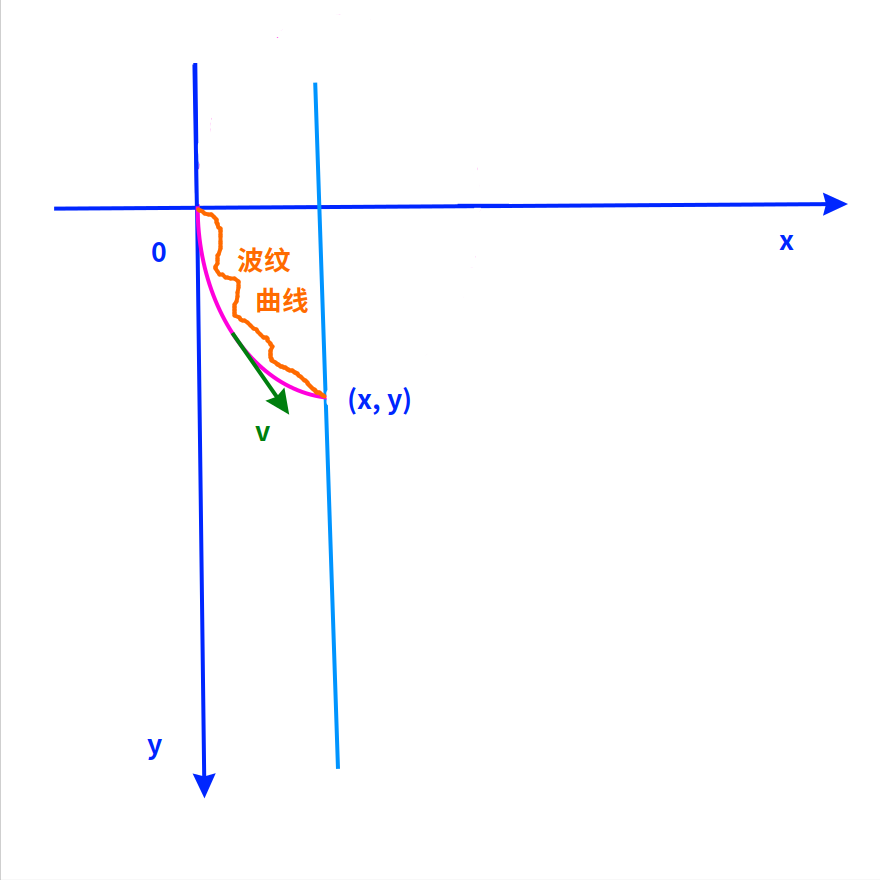
为了求出最速降线,我们假设已经求出了最速降线!
那么,只要曲线稍微有一点变动,时间就会增大。
这个方法就跟一元一次方程一样:要求某个未知数,就先设个未知数,假设它已经求出来了,然后让它直接参与运算
假设最速降线已经求出来了,任何微小的改变都会让时间增大,所以最速降线是时间的极小值:
可以把叫做y(x)的微小扰动,所以这种方法一般叫做微扰论,实际上就是反证法。
令 那么在微扰之后就变成了
时间t的改变量是微扰前后L的差对dx的积分。
在获得最优解的情况下,时间t的改变量应该为0,这种方法叫做变分法。

如果只把L按照y和y&39;的一阶导数展开,计算结果就是大名鼎鼎的欧拉-拉格朗日方程。
上图的左侧,就是欧拉-拉格朗日方程的推导过程(之前发过)。
上图的右侧,是把最速降线的公式代进去之后的结果:
如下图,化简之后,获得最速降线的微分方程 2yy&39;&39; + y&39; ^2 + 1 = 0.

解出来之后,获得x和y的参数方程,就是最速降线的解析式。
还可以进一步求出时间t的代数表达式来,如下图:

从可得
3,极限推理,
当起点-终点所在的两条竖直线极为接近的情况下:
最速降线趋近于直线,角度参数趋近于0,
正弦函数约等于角度:
(当x趋向于0时,sinx / x趋向于1)
也可以从x的参数方程看出来:
所以
也就是说:
t = (2y/g)^0.5,
y = 1/2 gt^2.
这与自由落体运动的位移时间公式是一样的。
所以,自由落体运动是最速降线的极限情况。
奋楫扬帆新征程!三明市加快推进革命老区高质量发展示范区建设侧记
立冬时节,走进三明处处洋溢着活力与激情高质量发展的热潮奔涌而来产业发展振奋人心,重大项目加速推进开放合作不断取得新突破……2022年3月,国务院批复同意建设闽西革命老区高质量发展示范区,三明革命老区发展迎来重大历史机遇。一年多来,三明奋楫争先,加快建设革命老区高质量发展示范区,在新征程上奏响奋进乐章。日新月异的三明城区(记者林文斌摄)转型升级培育高质量发展新动能大财经2023-11-21 18:02:360000燃气热水器十大名牌排名 燃气热水器第一名
NO1创昇太空能热水器创昇太空能创昇太空能热水器深受广大用户的喜爱和推崇。技术上的改革创新,环保节能环保节能的及时应用,这些努力使创昇太空能热水器从一个不知名的品牌发展到中国,成为世界上最大的太阳能制造基地和清洁能源供应商。公司主要致力于太空能热水器,空气能热水器,太阳能热水器,低温热泵,高温热泵,净水器等节能产品的研发与利用,为广大消费者提供安全节能,绿色环保,舒适方便的生活电器产品。大财经2023-03-21 02:53:020000“新开荒”酸菜事件:一场消费者与企业之间的“暗战”
嘿,大家听说了吗?最近“新开荒”酸菜可是在网上火了一把!原因竟然是它的包装上印有著名影星刘德华的照片。这一发现可让网友们炸了锅:刘德华是不是真的代言了这款酸菜呢?针对这个问题,“新开荒”酸菜的生产企业很快做出了回应:“所有手续齐全”。然而,这个回应并没有让消费者们满意,反而引发了更多的质疑。大财经2023-12-13 11:59:470000戎耀雄鹰!湖北老兵创业创新跑出加速度
极目新闻记者陈倩摄影记者刘中灿通讯员包晓霁常梦星从军营到社会,从军人到创业者,他们改变了人生的赛道,不变的是老兵的信念。十堰预膳食品科技有限公司董君君大财经2023-12-18 15:05:510000苏果,正在走下神坛的南京本土超市
提起苏果,每个南京人的都是熟悉的不能再熟悉。基本上每个小区门口,每条大街小巷都能看到苏果超市的身影。油盐酱醋,吃穿用度,南京人一年到头的吃喝拉撒基本都能在苏果得到解决。各企业的员工福利也都喜欢发苏果卡。苏果卡,金鹰卡,新百卡也长期占据着礼品回收店面的主要业务量。每年尾还会有打折促销活动,苏果里排长队和老头老太抢打折商品的场景每个南京人恐怕还记忆犹新。大财经2023-09-04 12:32:580000






