口腔溃疡怎么办最快最有效的方法 口腔溃疡是什么原因引起怎么治疗
说起口腔溃疡,不只是普通人,医生也是深受其害。拿我自己举例子来说,常年复发口腔溃疡,曾经一度每个月都会复发一次,喝水、刷牙、吃饭,甚至咽口水都疼,而且至少一周以上才会转归,可以说是苦不堪言啊。
什么?连医生都束手无策,那是不是就不用管它了?
口腔溃疡到底是个啥,怎么这么顽固?
听人说补充维C有用,是真的吗?

口腔溃疡,可以说是再常见不过的疾病了,人们有时候也叫它“口疮”,它有时候长在唇部,有时候在两颊软腭,有时候在牙龈,好像整个口腔黏膜都是它的“滋养床”。
医学上,口腔黏膜溃疡类疾病主要分为三类,即复发性阿弗他溃疡、白塞病和创伤性溃疡,我们常见的反反复复发作的那一类就是复发性阿弗他溃疡(RAU)。
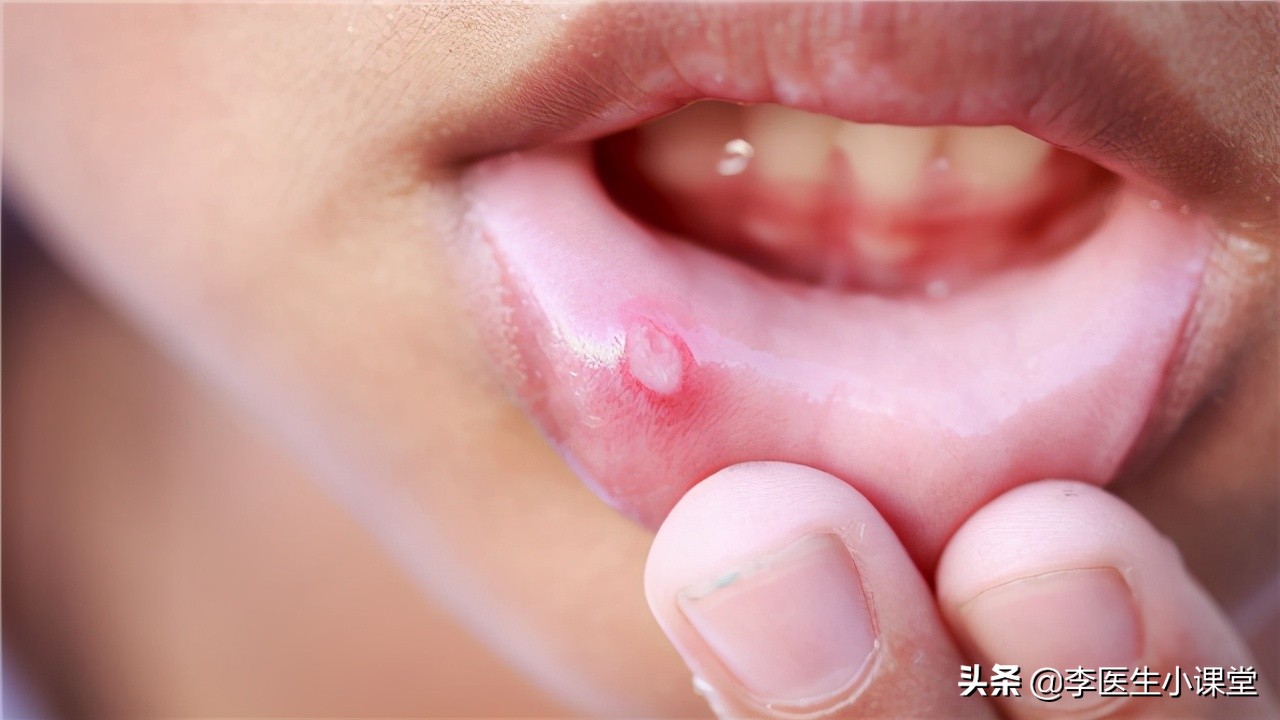
复发性阿弗他溃疡的典型特征是小而浅的圆形或椭圆形溃疡,表面覆盖有灰—白色假膜,周围黏膜红肿,溃疡部有灼烧样疼痛,总结来说就是四个字:“黄、红、凹、痛”。
有人说,口腔溃疡根本不需要去医院或者用药,自己也能好。的确,一般情况下,口腔溃疡7-14天就会愈合,而且不留瘢痕,但隔一段时间就会再发,这就是我们所说的它的另一特性,即“复发性、周期性、自限性”。
你是不是常常听到下面这些话:口腔溃疡又不是啥大毛病,吃点维C就好了啊;口腔溃疡就是上火;你要是不吃烧烤火锅,根本就不会生口腔溃疡……
但是,真的对吗?
口腔溃疡的病因十分复杂,我翻遍了资料也不甚明了,不是一句“上火、缺维生素”就能解释的。据研究表明,以下几种情况可能是引起该病的因素:
1. 消化系统疾病及功能紊乱:研究显示:口腔溃疡与胃溃疡、十二指肠溃疡、溃疡性结肠炎、局限性肠炎、肝炎等有关。比如30-48%的口腔溃疡患者有大大小小的消化系统疾病,其中有9%以上是消化道溃疡。
2. 内分泌变化:女性患者可能深有体会,每到月经期,就容易患上口轻溃疡,这跟经期雌激素水平的下降有关。
3. 心理及精神因素:当人体在精神紧张、心情抑郁、情绪激动或者睡眠不足的情况下,容易导致植物神经功能失调,这时,也容易诱发口轻溃疡。
4. 遗传因素:比如父母双方均患有复发性口腔溃疡疾患时,其子女同样得病的几率约为80-90%,若父母中一方患此病时, 子女患病可能性约为50-60%。
5. 其他因素:这就说到了为啥老百姓常说口腔溃疡补充点维C即可的问题了,因为人体在缺乏某种微量元素的情况下,比如维C、维B、锌、铁、叶酸等等,身体免疫力会下降,口腔溃疡也就更容易发生。

网上总是说用哪种药就能够消除口腔溃疡,不再复发,真的正确吗?大错特错!
通过上文,我们已经知道复发性口腔溃疡病因尚并不明确,所以目前仍无根治的特效方法。临床上,我们的治疗也是秉持消除病因、增强体质、对症治疗的原则,以此来减少复发次数,延长间隙期,减轻疼痛,促进愈合。
从药物选择上来说,主要是以下三类:
(1) 局部止痛类药物:比如临床上常用的利多卡因凝胶、复方苯佐卡因凝胶、苄达明含漱液等,多凃于创口表面或漱口用。值得注意的是,利多卡因凝胶副作用较少,但不适用于婴幼儿;复方苯佐卡因凝胶可能有一过性局部刺激症状,极少部分人可能出现高铁血红蛋白血症,2岁以下儿童禁用;而苄达明含漱液可能有头晕、胃酸分泌过多的情况;
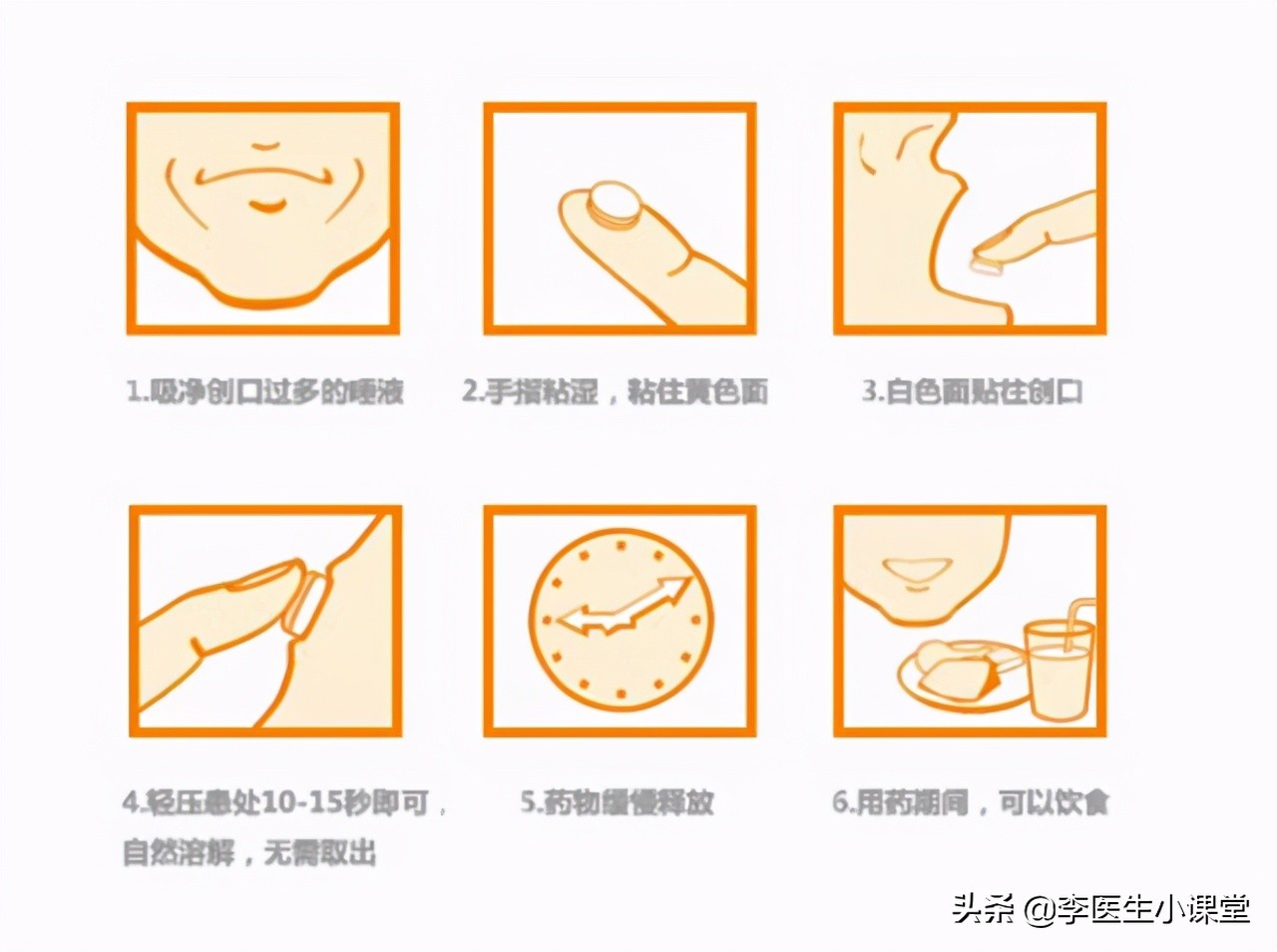
(2) 局部消炎药:如氯己定含漱液、倍氯米松含漱液、醋酸地塞米松贴片、西地碘片、氢化可的松或氢化泼尼松龙药膜等。
(3) 促进愈合药物:如常用的口腔溃疡散、冰硼散、西瓜霜、重组人表皮生长因子凝胶等。
以上药物大家见得多也用的多,但是我还是想补充三点:
1) 维生素B族 、 溃疡贴片、西瓜霜等,在用药之前最好先撕掉溃疡表面的那层假膜,这样可以保证药物更容易吸收,也可以减少感染;
2) 使用漱口水时最好先含在口中5分钟,后再吐掉,之后暂不漱口,30分钟内不宜进食或饮水,频次不可过高,一般每日3-4次为宜;
3) 局部使用激素类喷剂、散剂或者贴片时,尽量避免接触未发生溃疡的区域,也不宜长期使用,容易并发酵母菌感染。
以上均为局部用药,对于大多数非重型口腔溃疡十分有效,但对于发作频繁、症状较严重、甚至出现全身症状的患者,局部用药就不够了,需要全身治疗。通常来说,糖皮质激素、免疫抑制剂、免疫增强剂使用比较多,这类药物不建议自行购买,必须严格按医嘱用药,同时也可补充维生素,比如维C、维B等。
得了口腔溃疡需要正确治疗,没得也要积极预防:
1. 避免粗糙、质硬、过烫食物;规律进食、营养均衡,尽量少吃油炸、腌制、辛辣的食物;
2. 优质睡眠、情绪稳定、劳逸结合;
3. 注意口腔卫生,治疗胃肠道疾病。
医生总结:口腔溃疡反反复复,消除病因、增强体质、对症治疗、防治结合才是“王道”,治疗上不仅要秉承止痛、缩短病程、恢复口腔正常功能的原则,还要注意减少复发的频率及程度。
工大科雅(联合体成员鸿华建筑)成为哈尔滨市哈投集团智慧供热项目(二期)施工的中标人
2023年5月5日,工大科雅(301197.SZ)发布关于收到中标通知书的公告。2023年4月20日,河北工大科雅能源科技股份有限公司(以下简称“公司”)在巨潮资讯网刊登了《关于预中标公示的提示性公告》。近日,公司收到《中标通知书》,确定公司(联合体成员:山东鸿华建筑安装工程有限公司)为哈尔滨市哈投集团智慧供热项目(二期)施工的中标人。中标通知书主要内容如下:0001黑龙江旅游景点 黑龙江景区排名
羊草山位于黑龙江海林市长汀镇双峰林场“中国雪乡”景区内,最高峰为骆驼峰,海拔1235米,是雪乡最美丽的景点之一,因在这茫茫的原始森林中它的山顶树少草多而得名。由于羊草山的高度优势,再加上山上树木稀少,视野开阔,所以这里是观看日出、日落的绝佳地点。奇径碑园大财经2023-03-25 00:50:060003蚝油的作用和用法 蚝油的三种正确吃法
大家好,我是小楠。爱做饭的人,厨房里的瓶瓶罐罐肯定都少不了,蚝油肯定也在其中,不少朋友无论做什么菜都会用到,但是蚝油并不是万能的提鲜剂。蚝油是一种味道鲜美的调味料。由于生蚝可以让食物变得更鲜美,不少人就将蚝油当作生抽和酱油使用,不管什么菜都会放上蚝油,这样真的正确吗?大财经2023-03-22 04:54:210002和平精英怎么改名字 和平怎么免费改名字
提起将性价比做到极致的手机产品系列,必然少不了iQOONeo,自打诞生之日起就在实践着高性能和实惠售价的共存。在双11期间正式登场的iQOONeo7更是特别,用系列首次采用的联发科旗舰芯片实现高性能,售价有惊喜的同时也得到了不少游戏体验的下放。大财经2023-03-21 01:16:530000




