方差计算公式（方差的两个公式）

首先介绍一下什么是样条曲线？本质上，这是一种拟合模型 Y=f（X）+epsilon 的方法，f 是非参数的，由非常光滑的分段多项式构成。

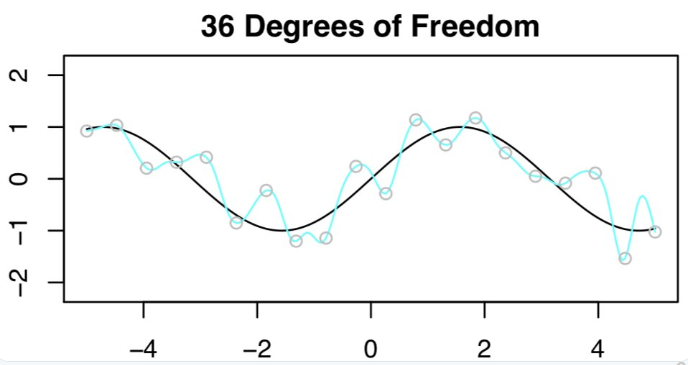
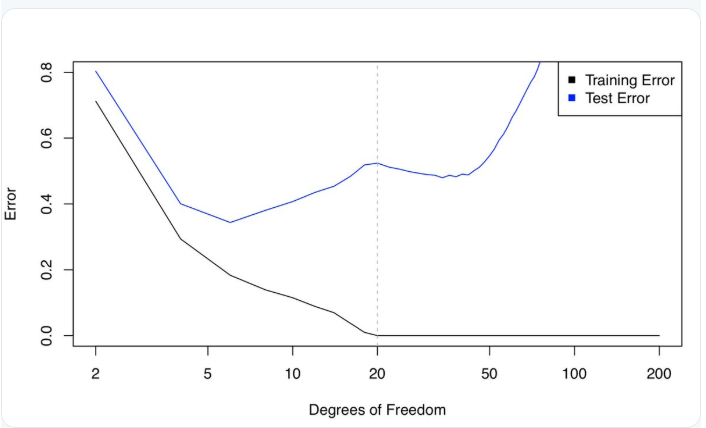
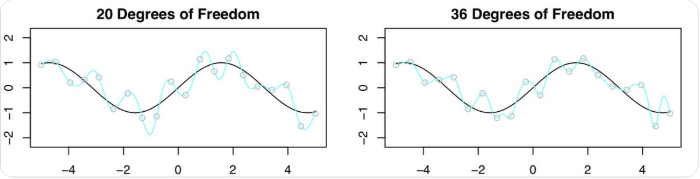
欣慰的是，结果并没有预期的那么糟。下图对比了 20DF 和 36DF 的结果，可见 36DF 的结果比 20DF 要好一点。这是什么原因呢？

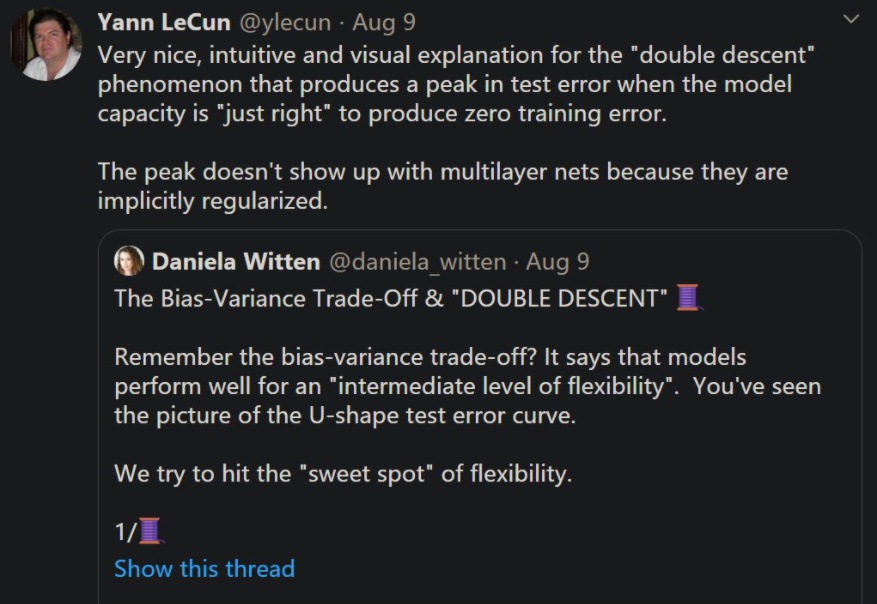
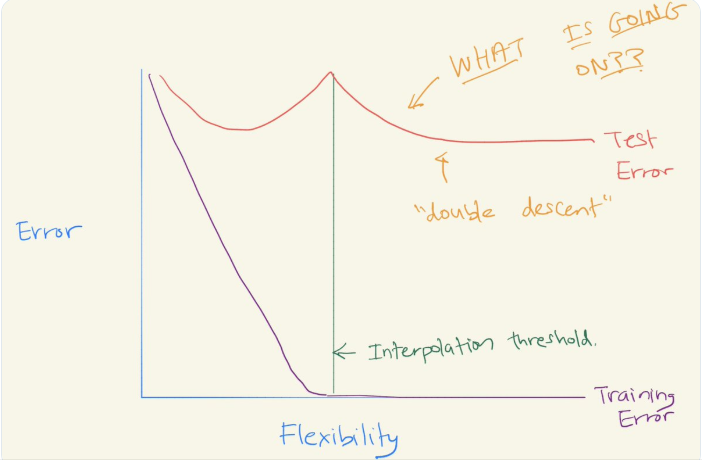
8 月初，华盛顿大学统计学与生物统计学教授 Daniela Witten 在推特上发帖介绍了「偏差 - 方差权衡」与「双下降」之间的关系。这个帖子一经发出便收获了很多点赞与转发。

上文中的 U 型测试误差曲线基于以下公式：

假设 n=20（X, Y），并且想用样条曲线 Y = f(X)+ epsilon 估计 f(X)（此处 f(X)= sin(X)） 。

因此双下降是真实发生的，并不是深度学习魔法。通过统计 - ML 和偏差 - 方差权衡可以理解它。一切都不是魔法，只是统计在发挥作用。

但是当增加 DF，使得 p>n 时，则会出现大量的插值最小二乘拟合。最小范数的最小二乘拟合是这无数多个拟合中振荡最小的，甚至比 p=n 时的拟合更稳定。

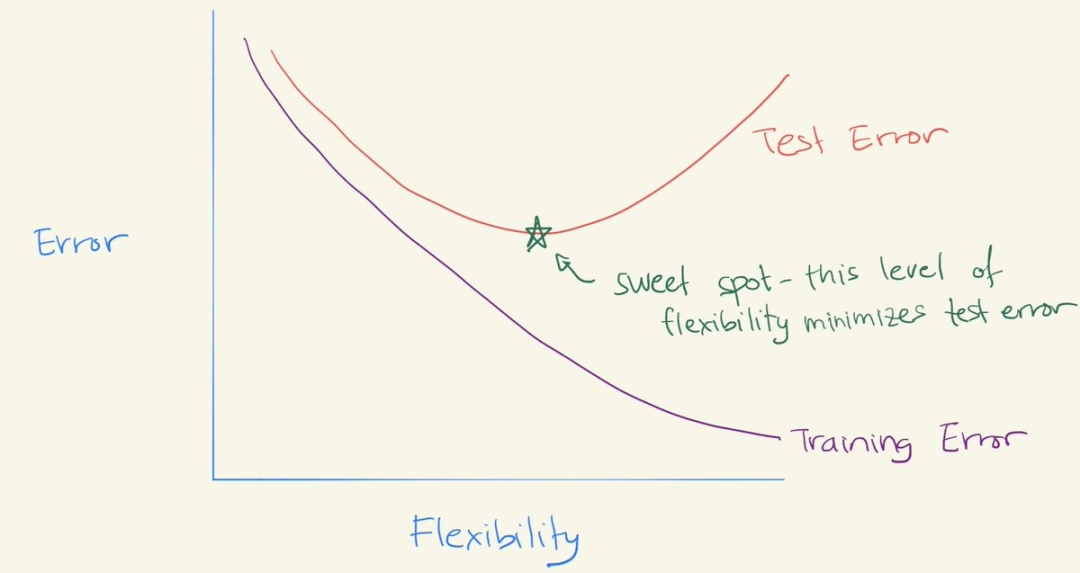
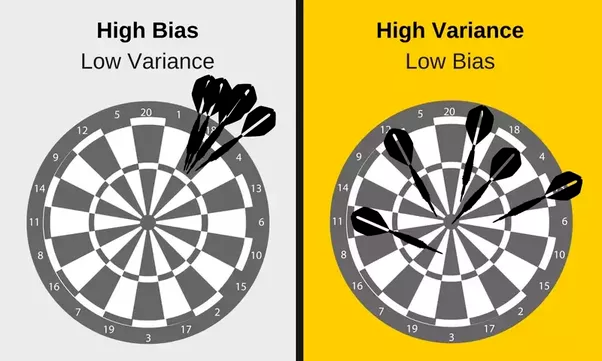
随着灵活性的增加，（平方）偏差减少，方差增加。「sweet spot」需要权衡偏差和方差，即具有中等程度灵活性的模型。

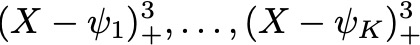
下图是训练误差和测试误差曲线，两者的变化曲线差别非常大。以虚线为分界线，当 p>n 时，为什么测试误差（暂时）减少？这难道就是偏差 - 方差权衡所指的对立面吗？

深度学习的双下降现象，偏差 - 方差权衡成立

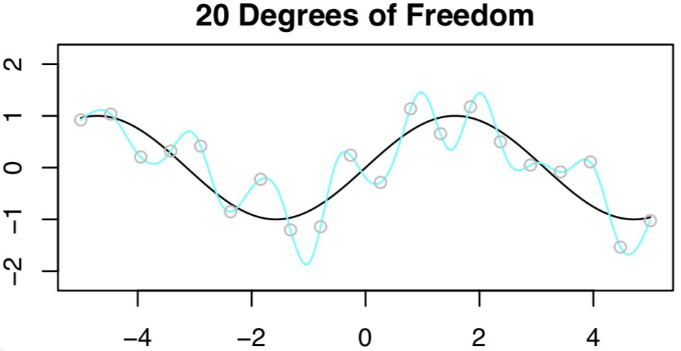
接着尝试拟合 20DF 的样条曲线，这不是一个好主意。因为得到了 n=20 的观测值，所以为了拟合 20DF 的样条曲线，需要用 20 个特征来运行最小二乘法！结果显示在训练集上零误差，但在测试集上误差非常大！这些糟糕的结果也非常符合偏差 - 方差权衡的预测。

为了拟合样条曲线，Daniela 等人创建了一些基函数，然后通过最小二乘法将响应（response）Y 拟合到基函数上。所用基函数的数量与样条曲线的自由度（degrees of freedom, DF）相同。基函数基本形式如下：

偏差 - 方差权衡不成立吗？

原文链接：

Daniela Witten 教授的解读究竟有哪些独到之处呢？她开篇是这样介绍的：「还记得偏差—方差权衡吗？它意味着模型在中等程度灵活性条件下表现良好。图中可以看到 U 形测试误差曲线。我们试图找到灵活性的『最佳点』（Sweet Spot）」。

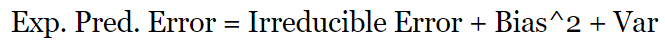
现在，如果在拟合样条曲线时使用了脊惩罚（ridge penalty），而不是最小二乘，结果会怎么样呢？这时将不会有插值训练集，也不会看到双下降，而且会得到更好的测试误差（前提是正确的调整参数值！）

这时 p>n，解是不唯一的。为了在无穷多个解中进行选择，Daniela 等人选择了「最小」范数拟合：系数平方和最小的那个（使用了大家最喜欢的矩阵分解 SVD，以实现轻松计算）

选自Twitter，作者：Daniela Witten，机器之心编译，编辑：陈萍、杜伟

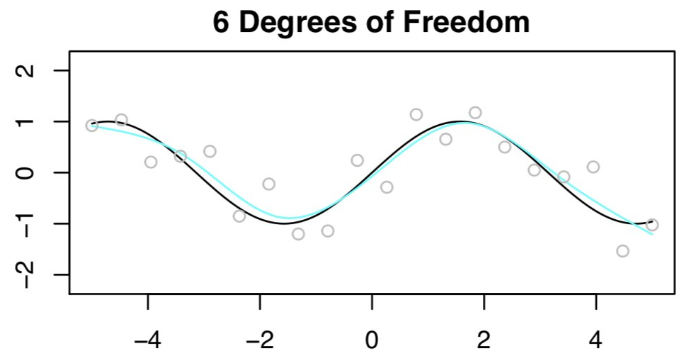
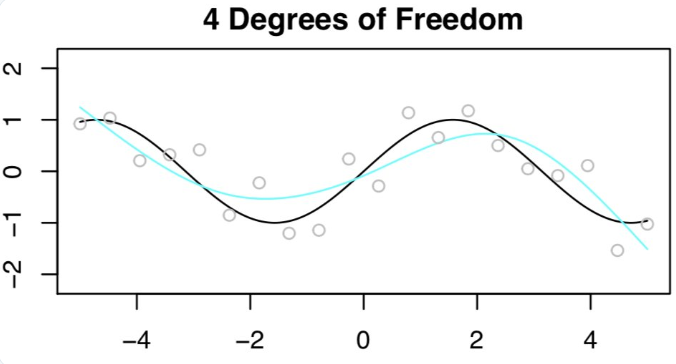
首先，Daniela 等人拟合了一个 4DF 的样条曲线。n=20 时的观测值为灰色小圆点，f(x) 为黑色曲线，拟合函数为浅蓝色曲线。

Daniela 等人给出了合理的解释：关键在于 20DF，n=p 时，只有一个最小二乘拟合的训练误差为零。这种拟合会出现大量的振荡。

总结

独到的偏差 - 方差权衡解读

偏差—方差之间的权衡判读对机器学习来说是非常重要的。在深度学习研究中，可能会遇到双下降现象，认为这有悖于偏差—方差权衡。本文通过一个统计学的例子，对偏差—方差权衡展开了形象的解读。

在深度学习的背景下，这一点似乎尤为突出（不过，正如我们看到的，这种情况在其他地方也会发生）。到底是怎么回事？偏差—方差权衡是否成立？教科书都错了吗？或者是深度学习的魔力？

在这篇帖子里，Daniela Witten 教授给出了合理的解释。为了理解深度学习的双下降现象，她列举了一个与深度学习无关的简单示例：自然三次样条曲线（natural cubic spline）。

过去的几年中，尤其是在深度学习领域，已经出现双下降现象。当你继续拟合越来越灵活且对训练数据进行插值处理的模型时，测试误差会再次减小！

所以，这些与深度学习有何关系？当使用（随机）梯度下降法来拟合神经网络时，实际上是在挑选最小范数解！因此，样条曲线示例非常类似于神经网络双下降时发生的情况。

AI 大咖 Yann LeCun 也转发了该贴，他高度称赞了 Daniela Witten 教授对「双下降」现象的解读。LeCun 写道：「这是对双下降现象非常直观的解释。当模型能力『恰好』能够产生零训练误差时，该现象导致测试误差达到峰值。并且，峰值不会出现在多层网络中，因为它们呈现隐式正则化。」

下图为 n=20，p=36DF 的拟合结果。

然后拟合了一个 6DF 的样条曲线。

虽然在 20DF 的测试结果非常差，但 Daniela 等人还是进行了 n=20，p=36DF 时的最小二乘法拟合。

http://threadreaderapp.com/origin/thread/1292293102103748609.html

所以，选择最小范数最小二乘拟合实际上意味着 36DF 的样条曲线比 20DF 的样条曲线的灵活性差。