三条有趣的概率问题(每一条都值得投资者反思)
2/3、公车问题与股池怪客
人的注意力资源是宝贵的,这一类股票一直在股池中,又很难被选中,其实非常浪费资源。要改变这种情况,有两个方法:
如果觉得前三题还是很简单,那最后的“终极问题”,只要理解了它,你就会对“择时”这件事,有更深的理解。
这跟投资有什么关系呢?你想,“生到男孩就结束”,这样就能提高生男孩的概率,这种说法是不是有点耳熟?
虽然老股民都知道这个方法的问题在哪儿,但事实上,确实有很多人一开始炒股票时,都这么尝试过,胡锡进说“只要亏了不卖,就不会被割韭菜”,这跟直觉中认为刚才生男生女的规则会导致男孩多或者女孩多,是一回事。

按直觉判断,连续抛掷三次硬币可以产生8种不同的结果,各占1/8。“正反反”和“反反正”获胜的概率当然是相同的。
很多新股民会跑过来跟我说:“我刚刚炒股几个月,一直都在赚钱,我的方法是亏了就拿着,直到赚10%就卖。我觉得炒股一点都不难啊,那些人一直亏是怎么回事?”
比如说,你的能力是擅长在财报中发现被低估的机会,或者在与公司交流中发现企业经营逻辑的长期变化,但你的弱点是缺少行业数据、下游客户调研、渠道调研的支持。
问题四:又是一题公车问题,你每天都要坐一路公交车,极其不准时,发车时间完全随机,有时长达几个小时不发车,有时两班一起发,按近一年的统计规律,平均每10分钟发一班车,请问你一年坐下来,平均每次要等几分钟?
第二题:1路公交车和2路公交车的发车间隔时间都是10分钟,路线和速度完全相同,它们都会路过你家门口的某个站台,每天你在不固定的时间去车站等车,哪辆车先来就上哪辆。可能有人认为,你坐到这两路车的概率应该是一样的,可长期观察下来,你发现自己坐上A路车的概率是B路车的9倍——为什么?
既然是开胃菜,结论并不难猜,当然是男孩女孩各一半。
然而正确答案却是:虽然“正反反”和“反反正”出现的概率是相同的,但如果你选“反反正”的话,赢的概率就只有对方的三分之一。
2、定期剔除股池里那些永远选不上的标的
我们可以换一个立场,从医院的角度,每一个进来的孕妇,不管是初育还是再育,不管之前生的是男孩还是女孩,生下来的孩子性别都是概率对等,那么长期积累下来就应该是对等的。
这个概率问题跟投资大有关系,决策判断有时也是一个时间顺序的比拼。
在A股这个极度内卷的市场,比拼的早已不是你能不能发现机会,而是能不能率先发现机会,又要保持高胜率。
答案:虽然两路车都是10分钟一班,但1路车的到站时间是8:09, 8:19, 8:29……,而2路车的到站时间是8:10, 8:20, 8:30……,每次刚好晚一分钟,导致你坐上2路车的概率只有1路车的1/9。
基于上面的两个理由,利好出现的顺序非常重要,尽可能跟踪一些逻辑信号出现的顺序对你有利的股票,放弃对你不利的股票。
概率现象与投资之一
3/3、硬币问题与选股抢答
首发于“思想钢印(ID:sxgy9999)”微信公众号,讲述价值投资的理念和方法
2、有投资机会的股票之前一定会出现一系列信号,但基于上面的原因,等到所有信号都出现了再买,就来不及了,最好是只要你认为最重要的那个信号出现,就可以下手;放弃也是如此,你不能等到刮出“谢谢惠顾”才放弃,一定是看到半个“谢”就知道放弃。
但是,很多人都有这个感受,有一些股票,就是“一直被看好,从未被选中”,原因跟刚才的公车问题很类似,很多人选股的标准非常单一,导致股池里的品种也非常类似,结果总有一两支股票,就是那个永远晚一分钟的2路车,当出现机会的时候,别的股票比它更有机会;别的没机会的时候,它也没机会。
在这种情况下,你就要避开有高频数据的行业,在这些行业中,你发现的机会,往往之前的高频数据已经体现出来,那些更擅长从高频数据中挖掘投资机会的投资者早已先行一步,结果要么是你觉得估值太高,要么是“价值陷阱”。
这个题有点绕,一时想不通的,可以在纸上多模仿几次,就知道问题出在哪儿了。
某个国家有一个奇怪的政策:每对夫妇如果生出的是男孩就要被绝育,如果生出的是女孩就必须继续生下去,直到生出第一个男孩儿为止。这个政策执行很多年后,该国的男女比例会发生怎样的变化?
好的,开胃菜结束,问题开始升级。

跟前题一样,这个游戏比拼的并不是“出现的概率”,而是“谁先出现的概率”。
1、选股思路可以开放一些,不要总是选同一类品种
这个概率问题跟股票投资有什么关系呢?
1、每一支股票,总有很多投资者跟你一起研究,很多人的研究能力不在你之下,一个投资机会,发现的人多了,股价就涨起来,此时你再发现,很可能没有性价比。
我猜类似的问题,很多人都思考过,这个问题有两种相反的直觉判断:
还有人认为是女孩多,因为这种“不生男孩不罢休”的政策,必然会出现很多家庭一直生不出男孩,家里一堆女孩。

之所以直觉会有偏误,是因为概率是基于整体的分析,而我们直觉都是从个体的经验,选择最常出现的家庭类型进行判断。
问题三:你和你媳妇儿都不想扫地,最后决定通过抛硬币来确定。不过,你媳妇儿觉得太无聊,提出“乐趣版”改进方案:连续抛掷硬币,直到最近三次结果是“正反反”或者“反反正”。如果是前者,她获胜,你扫地;如果是后者,你获胜。她扫地。
这句话,前后并不矛盾,请注意本题的叙述“连续抛掷……直到……”,隐藏着一个“陷阱”——顺序。
有人认为男孩多,因为该政策会导致最后一个孩子大部分是男孩,而前面的孩子男女比例相同,比如有两个家庭,一个生了男孩,另一个生了女孩后又生了一个男孩,结果就是2比1;
你(“反反正”)想要获胜,就要抛出两个“反”,但在这个两个“反”之前,只要先抛出一个“正”,你媳妇儿就已经先赢了,根本不会给你机会。换言之,你想要赢,就要在游戏的第一、二次连抛两个“反”,如果出现的是“正正”、“正反”、“反正”中的一个,无论接下来出现什么结果,对方都必胜,所以你获胜的概率只有对方的三分之一。
好了,两道初级问题分析完了,下面的问题要开启“烧脑模式”了:
本题看似简单,实际上与几个重要的概率理论有关,解释的复杂程度也更高,对于投资也更重要,因此有必要单独写一篇在下周,特此预告。
1/3、生男政策与新股民幻觉
之所以直觉与实际情况背离,因为直觉比较的是“到站的概率”,而实际生活中,这是一个“谁先来的概率”的顺序问题。
看上去这个规则很公平,但考虑到你媳妇儿是程序员,当年的数学竞赛冠军,你还是怀疑她在给你下套。到底是不是呢?
假如你总是同时持有四支股票,如果有一支涨得太多,或者逻辑破了,你就卖出,换成股池里10支股票中目前相对看好的一支,假定每一支股票加入股池时的看好程度都差不多,而且,股池里的股票如果涨得太多,也会被你剔除,那理论上说,每一支股票在换股中被挑中的概率是差不多的。
先来一道开胃前菜:
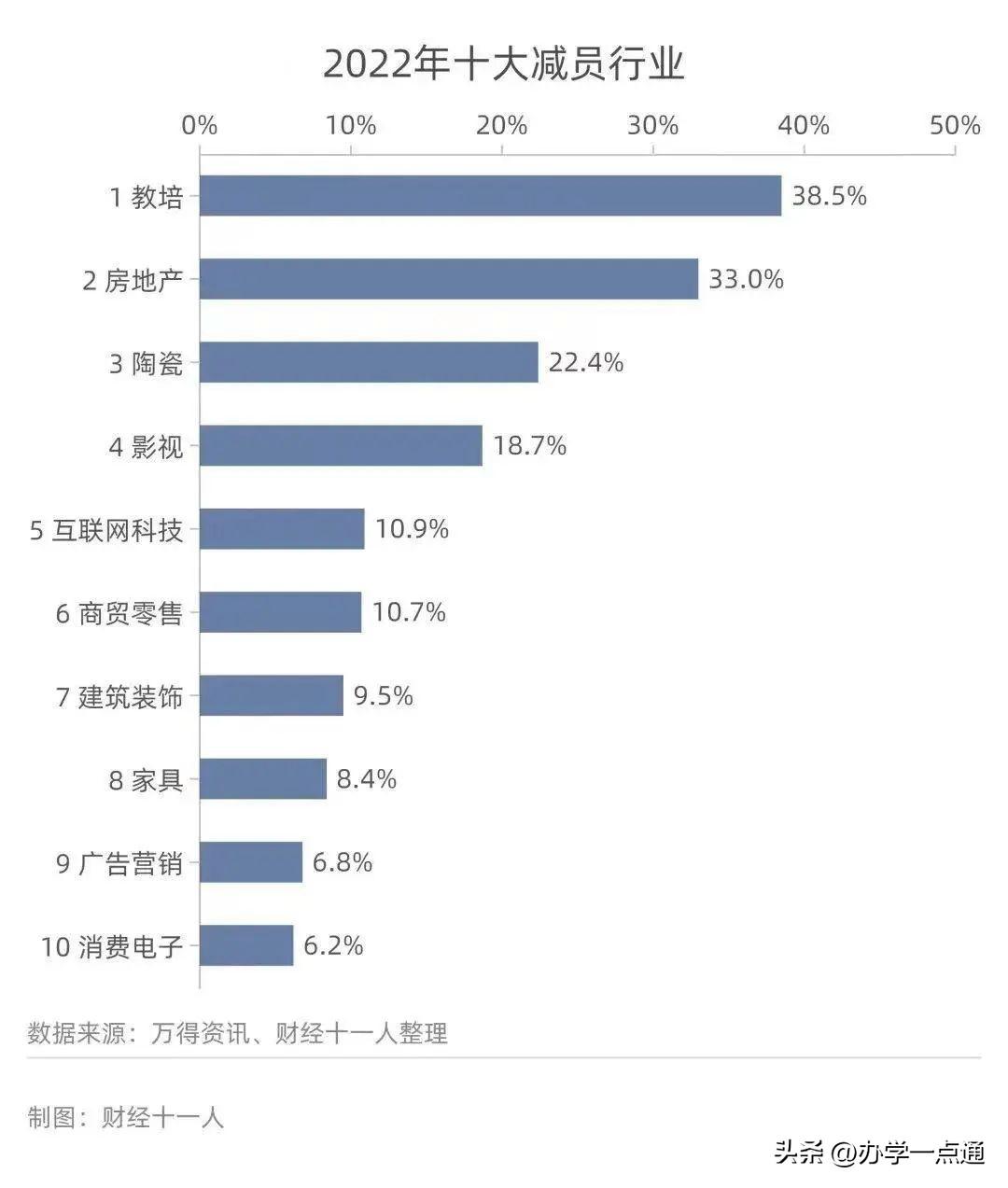
2022年十大减员行业公布:教培行业居首位
第二名房地产行业减员33%2022年是中国房地产行业的至暗时刻,行业惨状无需多言。房地产是周期性行业,但从2000年开始,中国房地产行业整体波动上升。2022年是一个分水岭。2022年之后,绝大部分城市的房子不再是稀缺商品。大财经2023-05-18 17:36:530001美国经济前路难测:银行业危机汹汹 债务僵局还来添乱
美国经济当下的复杂局面正在让越来越多的经济学家和分析师感到焦虑。本周四,美联储将公布5月利率决议,而在加息与否的关键议题之外,市场还在担忧美国政府的债务违约可能性。周一,美国财长耶伦警告,政府最快可能在6月1日耗尽资金并引发经济危机。这一时间点比市场预计的6月末、7月要更加提前。0003中国汽车出口:欧盟骤降,东南亚“井喷”
近日,乘联会秘书长崔东树对11月中国汽车出口走势分析,表示11月单月的新能源车出口仅15.3万台,增速剧烈放缓到6%。数据显示,2023年前11月,累计出口新能源车继续攀升至160万台,同比增长87%。显然,与前11月累计出口量的高速增长不同,11月中国汽车出口急速“降温”。大财经2023-12-28 20:19:410000