中国突破10亿吨油田大发现?全球能源格局将如何改变?
中国石化集团并没有被这些困难吓倒,他们积极调整策略,采取了一系列创新技术和措施,以克服挑战。这种方法通过地震仪器将地震波传播到地下,然后根据不同介质的反射和折射特性,来推断地下的岩层结构和石油储量。三维地震勘探相较于传统的二维勘探更加精确和全面,它可以提供更多的地质信息,为勘探人员提供更准确的数据支持。

水平井开采技术是一种油田开采方法的革新。以往的油井都是竖井,沿着储层的垂直方向进行开采。而水平井则是在储层中开凿水平段,通过增加水平段的长度,大大增加了储层与井筒的接触面积,从而提高了油田的开采效率。水平井开采技术还可以在较远的距离内进行岩石破碎,进一步增加了石油的产量。
利用三维地震勘探和水平井开采技术,中国石油化工集团公司成功筛选出了玛湖油田,这是一项令人瞩目的成就。

玛湖油田位于我国西北地区,地处一片荒芜而广阔的大漠之中。这里曾经是一个不毛之地,没有人烟,也没有任何生命的痕迹。但是,随着中国石油化工集团公司的到来,这片土地焕发出全新的生机和活力。
玛湖油田的发现对于中国的能源战略意义重大。在当前全球经济竞争日趋激烈的背景下,能源供应是中国持续发展的一大难题。然而,玛湖油田的发现,为中国提供了一次绝佳的机遇。

当地政府和企业紧密合作,利用当地丰富的太阳能资源,建设了一座巨大的太阳能光伏发电站。这座发电站负责为玛湖油田提供稳定可靠的电力供应,使得这座油田成为全球首个完全依靠太阳能发电的油田。
玛湖油田的发现不仅解决了能源供应问题,还创造了大量的就业机会。当地村民转行成为油田工人,他们参与到油田建设中,学习新的技能,提高了自己的综合素质。同时,油田建设带动了当地的经济发展,使得玛湖油田周边的小城镇焕发出勃勃生机。

玛湖油田的建设还以环境保护为前提。中国石油化工集团公司充分重视环境保护,采取了一系列措施来确保油田的开采过程对环境的影响最小化。他们利用先进的油田治理技术,对油田废水进行处理,确保排放达标。同时,他们还建设了一座大型的生态公园,用来保护当地的生物多样性和生态平衡。
玛湖油田的发现是中国石油化工集团公司勘探技术和环保意识的结晶。它不仅证明了中国企业在勘探技术上取得了重大突破,也彰显了中国在能源领域的实力和责任。

玛湖油田的发现是一段传奇,它让那片荒芜的大漠焕发出新的生机和活力。它让中国人民在能源领域迈向了一个新的里程碑。玛湖油田,见证了中国梦的力量,也见证了中国石油化工集团公司的智慧和勇气。让我们一起为中国的能源事业欢呼,为中国企业的创新和奋斗点赞!
为了解决高海拔区域带来的寒冷问题,中国石化集团研发了一种独特的特殊油井保温液。这种保温液能够有效地降低油井温度,并防止水分蒸发。通过使用这种保温液,他们成功地解决了在极寒地区开采的难题,保证了油气的正常开采。

为了应对干燥的地质环境,中国石化集团投入大量精力研究储气库建设。他们充分利用地下地质层的特点,建立了一套完善的储气设施。这些储气设施可以收集并储存来自油井的天然气,以应对供应短缺和需求高峰,保证了能源的稳定供应。
中国石化集团还大力推行“绿色开采”理念,注重环境保护和可持续发展。他们采用了高效的油气开采技术,最大限度地减少了对周边生态环境的影响。与此同时,他们积极开展环境监测和治理工作,保护了当地生态环境,助力了地方可持续发展。
在中国石化集团的努力下,玛湖油田取得了巨大的成功。油气勘探和开采取得了突破性进展,使得中国能源供应局面得到了明显改善,也为中国经济的可持续发展提供了强大的支持。

玛湖油田的发现也引发了全社会的关注和热议。这不仅仅是因为石油产业的重要性,更是因为中国石化集团在克服困难、创新发展方面所展现出的卓越能力。他们的勇敢探索和不懈努力值得我们学习和赞美。
中国石化集团在玛湖油田的发现中,不仅仅是一个在地质领域的惊奇,更是一个在技术领域的革命。他们的创新技术和勇往直前的精神,为我们展示了中国企业追求卓越的决心和智慧。

希望随着时间的推移,中国石化集团能够继续取得更多的成功,并为中国的能源事业和经济发展做出更大的贡献!让我们共同期待玛湖油田的再次创造奇迹,为中国的发展打造更加美好的未来!
文章描述过程、图片都来源于网络,此文章旨在倡导社会正能量,无低俗等不良引导。如涉及版权或者人物侵权问题,请及时联系我们,我们将第一时间删除内容!如有事件存疑部分,联系后即刻删除或作出更改。
山东潍坊楼市的危机,房价低廉的潍坊楼市潜力与未来
山东省是我国的经济大省,也是我国的人口大省,对于这个区域而言,青岛的综合实力排名第一,其次是烟台、济南、潍坊。潍坊的实力有多强,或许很多本地人不太认可,但潍坊的确在全国的排名相当靠前。在过去的2022年,潍坊共完成经济总量7,469亿元,在全国300多个城市当中名列第34位。与潍坊经济总量在300亿元左右的城市主要有:厦门、沈阳、昆明、绍兴、南昌、扬州、石家庄的等。大财经2023-04-17 16:02:310000高密度脂蛋白 高低密度脂蛋白血症
来源:央视一套随着生活节奏的加快以及饮食习惯的变化高血脂人数不断增加哪些症状是高血脂的表现?如何通过饮食控制血脂?一起来看看↓↓↓血脂的主要成分是啥?血脂的主要成分是甘油三酯和胆固醇它们都是维持人体机能不可缺少的物质胆固醇又分为高密度脂蛋白和低密度脂蛋白动脉硬化的形成低密度脂蛋白增高是“主犯”甘油三酯偏高是“从犯”想要控制血脂主要应控制胆固醇的摄入0001娇艳欲滴的意思 翠绿欲滴的欲的意思
搜索作者/云开日初——娇艳欲滴朵朵鲜,貌美如花美缱绻。国色天香婉约女,含情脉脉淑女范。我们相遇即是缘,在千千万万的文章里,你若偶然与我的文字相遇相见,我们就是特别的缘分,感恩遇见!感恩你的关注!感恩你的支持与点赞!也感恩那些默默无闻来到我家园的读者!更希望来访的各位朋友指导并提出宝贵意见!剪辑制作/诗文/云开日初——大财经2023-03-25 09:23:080001央媒看南阳|人民网、农民日报等央媒聚焦南阳市“四好农村路”建设及“三夏”生产——喜见新变化 凝聚新动能
近日,人民网、农民日报、中国农网等央媒,聚焦方城县“四好农村路”建设、唐河县“三夏”生产等,充分展示了我市深入推动交通运输事业发展取得的新成就,有力彰显了南阳坚决扛稳粮食安全重任的担当作为。0000分布式操作系统 分布式系统是什么意思
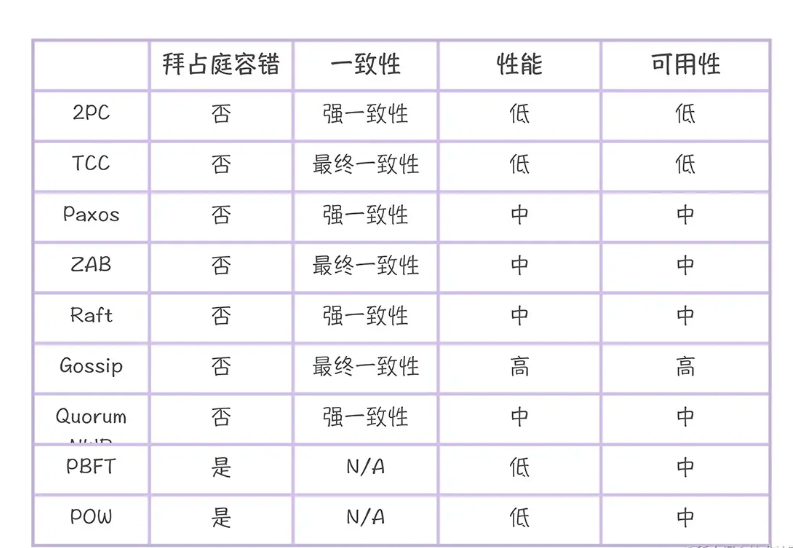
开发分布式系统最关键的就是根据场景特点,选择合适的算法,在一致性和可用性之间妥协折中,而妥协折中的关键就在于能否理解各算法的特点。我们讲分布式系统的一致性,一般来说,有如下几个分类:大财经2023-03-25 01:22:070000