自由落体公式 自由落体加速度公式
搜索群星10月榜
自由落体运动,物体仅受重力的作用,沿着竖直线下落。
早在万历年间(1572-1620),伽利略就通过比萨斜塔实验,发现了自由落体定律。
1685年,牛顿在“自然哲学的数学原理”中,提出了牛顿三大定律。
根据牛顿第二定律,mg = ma,自由落体加速度 = 重力加速度g。
(自由落体加速度表达的是惯性,重力加速度表达的是引力)
自由落体运动的速度 v = gt,位移 s = 1/2 gt^2.
如果下落的起点与终点之间的高度差为y的话,那么所需要的时间 t = (2y/g)^0.5。
起点与终点在一条竖直线上,不需要微积分,只用简单的二次代数方程就可以算出来。
但是,如果起点和终点不在一条竖直线上,这个问题就会变得很复杂,甚至在1696年被伯努利拿来考验牛顿
这就是最速降线问题。
1,最速降线问题,
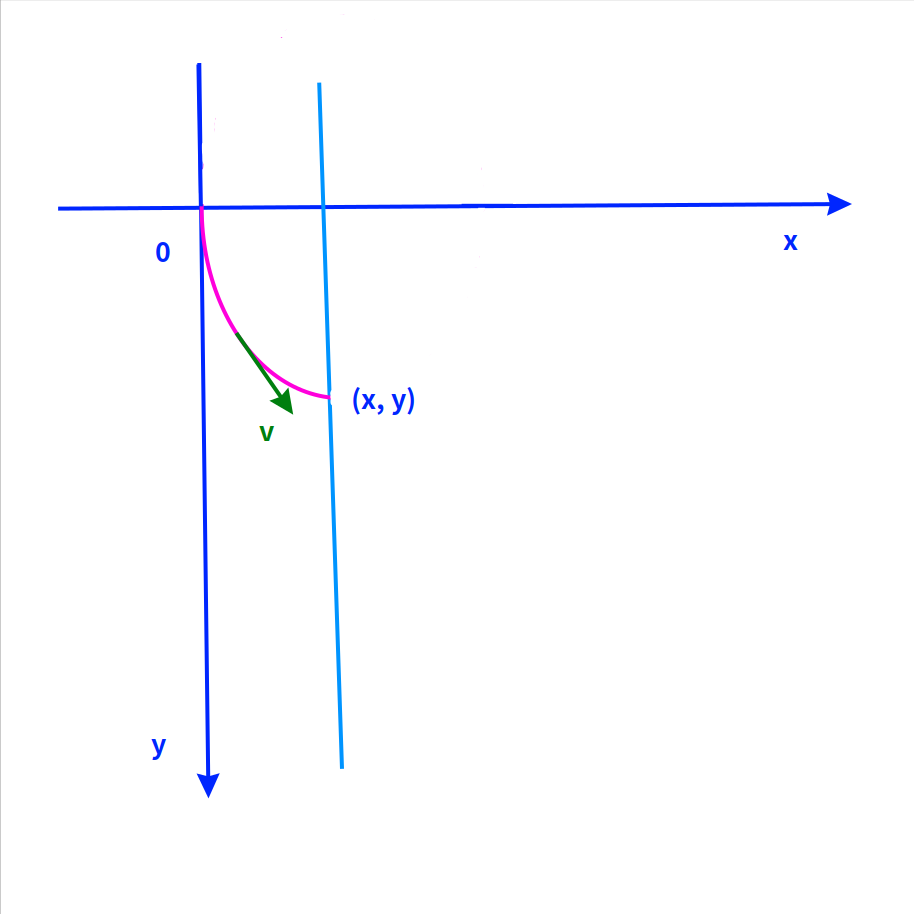
如图,不管在不在一条竖直线上,根据能量守恒定律,速度的值都是 v = (2gy)^0.5。
速率与x坐标是没关系的,因为重力做功只和高度差有关,与路径无关。
只是不在一条竖直线上时,速度的方向是变化的。
但不在一条竖直线上时,曲线的切线方向也是变化的。
并且,速度的方向始终沿着曲线的切线方向,所以它依然是个均匀加速的问题。
只是这么稍微一偏之后,就得使用微积分了:
而且,就算使用了微积分之后,问题依然不好解决。
两点之间的直线只有一条,但两点之间的曲线有无数条。
到底哪一条曲线是最节省时间的?
2,反证法、微扰论,
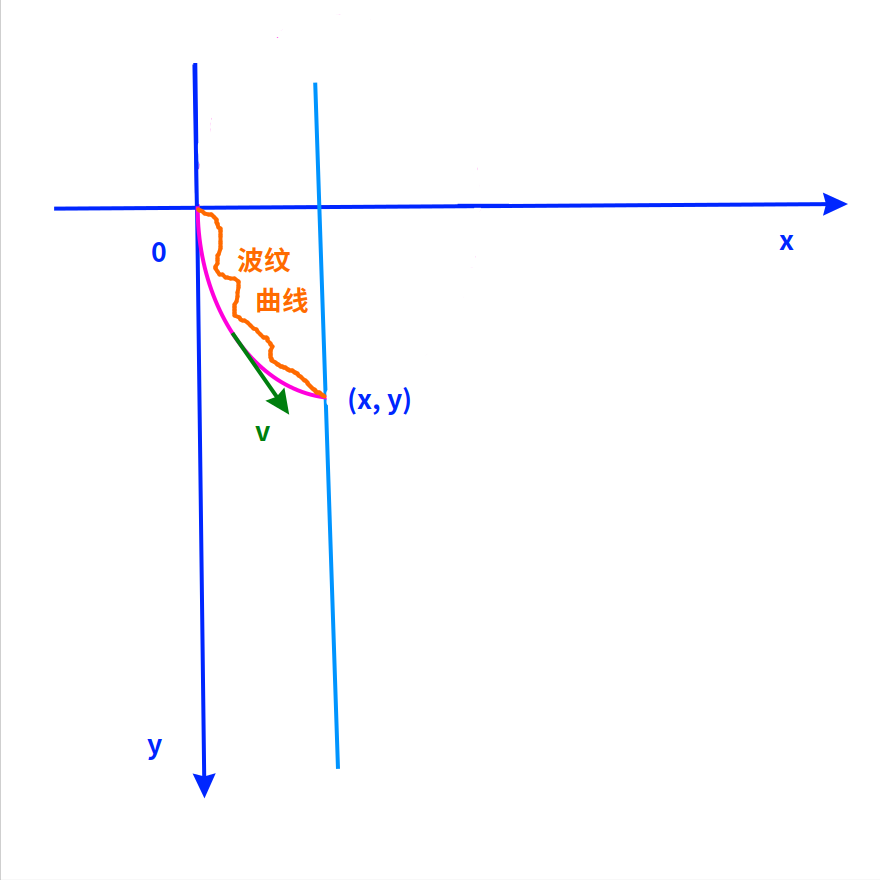
首先,最节省时间的曲线一定是光滑的,不可能是波纹状的。
因为,在非常微小的间隔内,速度可以认为是近似不变的,而波纹状曲线比光滑曲线具有更大的弧长。
显然,ds = vdt,波纹状的ds更大,所以肯定更费时间。
所以,最速降线的一阶导数肯定是连续变化的,而且一阶导数不能有极值点,也就是说二阶导数不能有零点。
否则,就成了波纹线了:只要把它稍微取直,花费的时间就会减少。
为了求出最速降线,我们假设已经求出了最速降线!
那么,只要曲线稍微有一点变动,时间就会增大。
这个方法就跟一元一次方程一样:要求某个未知数,就先设个未知数,假设它已经求出来了,然后让它直接参与运算
假设最速降线已经求出来了,任何微小的改变都会让时间增大,所以最速降线是时间的极小值:
可以把叫做y(x)的微小扰动,所以这种方法一般叫做微扰论,实际上就是反证法。
令 那么在微扰之后就变成了
时间t的改变量是微扰前后L的差对dx的积分。
在获得最优解的情况下,时间t的改变量应该为0,这种方法叫做变分法。

如果只把L按照y和y&39;的一阶导数展开,计算结果就是大名鼎鼎的欧拉-拉格朗日方程。
上图的左侧,就是欧拉-拉格朗日方程的推导过程(之前发过)。
上图的右侧,是把最速降线的公式代进去之后的结果:
如下图,化简之后,获得最速降线的微分方程 2yy&39;&39; + y&39; ^2 + 1 = 0.

解出来之后,获得x和y的参数方程,就是最速降线的解析式。
还可以进一步求出时间t的代数表达式来,如下图:

从可得
3,极限推理,
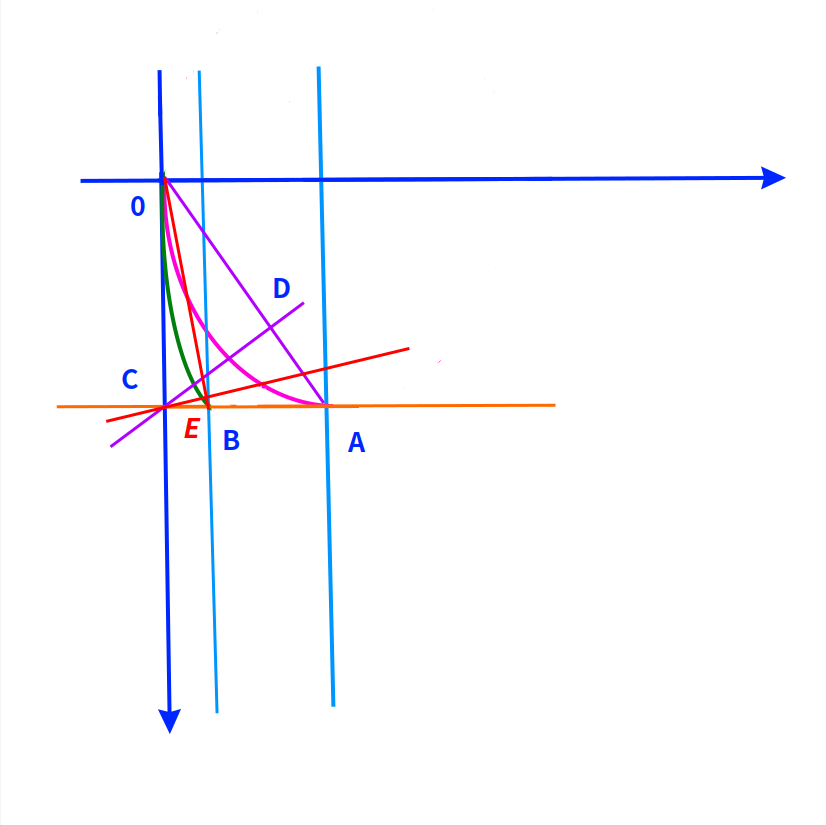
当起点-终点所在的两条竖直线极为接近的情况下:
最速降线趋近于直线,角度参数趋近于0,
正弦函数约等于角度:
(当x趋向于0时,sinx / x趋向于1)
也可以从x的参数方程看出来:
所以
也就是说:
t = (2y/g)^0.5,
y = 1/2 gt^2.
这与自由落体运动的位移时间公式是一样的。
所以,自由落体运动是最速降线的极限情况。
普通人的生活困境:收入与生活成本的博弈
在这个繁华的社会里,每个人都在为生活奔波。然而,对于大多数普通人来说,生活的不容易并非只是一句空洞的话语,而是实实在在的压力和挑战。这些压力和挑战,主要来自于高房价和房贷、教育成本、收入状况、老龄化人口和养老负担、医疗支出以及日常开销等方面。大财经2023-12-04 14:52:250000你就是“汪小姐”吧?
潮新闻记者拜喆喆电视剧《繁花》,最近是浙江外贸人聊天群里的热门话题。“外滩27号”,唤醒了一代人共同的记忆。外贸企业浙纺集团业务员宋梅的老友群里,更是分外热闹:宋梅所在群里“老外贸”们的讨论。来源:受访者提供宋梅也在追《繁花》,剧中的每一幕,都勾起了她对那个时代最初的回味。元旦后第一天上班,年轻同事们“八卦”地围住了宋梅:“宋老师,你是不是《繁花》里的‘汪小姐’啊?”大财经2024-01-10 12:48:520000⚠️非常警惕一个板块的巨大风险#大咖观察
非常警惕一个板块的巨大风险。受抖音、西瓜、头条深一度的邀请,我们来提醒一下风险。有很多的听众朋友抱怨,我为什么不经常提醒风险?其实我提醒风险的是在每一期都是提醒风险的,只不过很多人视而不见。大财经2023-12-29 02:13:330000网游类小说 网游重生类型的小说
大家好,我是鹏哥,今天给大家推荐十大公认网游小说神作推荐,老书虫本本耳熟能详,书荒了再看一遍第一本:《网游之纵横天下》作者:失落叶书评:这本书是月恒三部曲之一,主角丁书生,在游戏灵恸里升级历练,最终天下无敌,不论是女性角色刻画、剧情流畅度方面都相当成熟。这绝非一本完美无瑕的网游作品,但它仍是无数网游小说迷心中的神作。数据详实代入感强,值得一读!第二本:《网游之近战法师》作者:蝴蝶蓝大财经2023-03-25 08:57:240002线上短视频“引流”、线下“游击队”上门 “高科技”防水补漏实为噱头
来源:中国消费者报图一:打孔注胶后,吴女士家卫生间瓷砖出现裂纹。图二:记者咨询一家“五星”网店,对方声称不需要实体店。大财经2023-06-05 23:10:360000