中国人民保险集团:前10月原保险保费收入合计约5759.18亿元
大财经2023-03-21 18:14:141阅
e公司讯,中国人民保险集团在港交所公告,2023年1月1日至2023年10月31日经由公司子公司中国人民财产保险股份有限公司(“人保财险”)、中国人民人寿保险股份有限公司(“人保寿险”)及中国人民健康保险股份有限公司(“人保健康”)所获得的原保险保费收入分别为4398.07亿元、945.26亿元及415.85亿元。
0001
相关推荐
95508是什么电话 95508打我电话干嘛
日前,有关部门公布了多起养老诈骗案例。案情显示,不法分子瞄准“银发”群体的养老需求,以销售“养老金融产品”、投资“养老项目”、开展“养老帮扶”等为名进行诈骗,窃取老年消费者银行账户敏感信息或盗取账户资金。0000说明方法有哪些? 小学常用说明方法
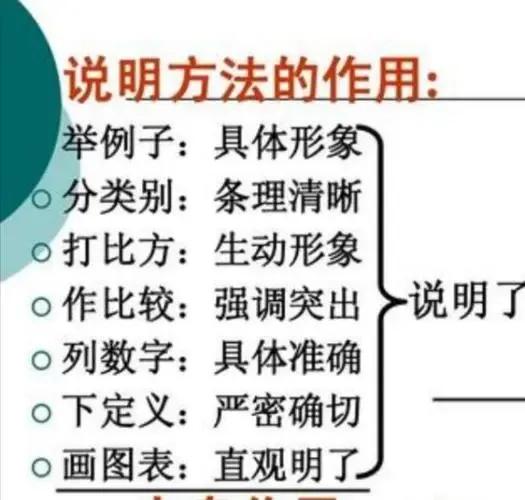
1、举例子。为了便于读者理解文中内容,作者根据具体描述的事物,举出一个详细的案例来进行阐述。2、分类别。对于要进行说明的对象,根据一定的规则进行分类,便于理解。例如我们在介绍英短猫的时候,为了方便说明,可以说它属于猫科动物,这样就很容易进行理解。大财经2023-03-20 20:28:410000投资日历:周四资本市场大事提醒
0000春晓的意思全解 春晓表达了什么
春眠不觉晓,处处闻啼鸟。夜来风雨声,花落知多少?这首朗朗上口的古诗,想必无人不知,无人不晓,它描绘了一幅怎样的景象呢?作者又是谁呢?我们先来解释下这首诗,这首诗的意思是:春天睡醒不觉天已大亮,到处是鸟儿清脆的叫声。回想昨夜的阵阵风雨声,吹落了多少芳香的春花。由此可见,这首诗描绘的是春天一场雨后的景象,有鸟儿的啼叫声,有洒了一地的春花。大财经2023-03-22 04:21:150001巴菲特100万美元“打赌”!事关美国储户→
本文字数:930,阅读时长大约2分钟导读:“股神”称,管理层应该为银行经营不善付出代价。作者丨第一财经樊志菁伯克希尔哈撒韦董事长、“股神”巴菲特周三表示,尽管硅谷银行和签名银行最近倒闭引发了担忧,人们不应该对银行业或存款的安全感到恐慌。大财经2023-04-16 12:09:420000