自由落体公式 自由落体加速度公式
搜索群星10月榜
自由落体运动,物体仅受重力的作用,沿着竖直线下落。
早在万历年间(1572-1620),伽利略就通过比萨斜塔实验,发现了自由落体定律。
1685年,牛顿在“自然哲学的数学原理”中,提出了牛顿三大定律。
根据牛顿第二定律,mg = ma,自由落体加速度 = 重力加速度g。
(自由落体加速度表达的是惯性,重力加速度表达的是引力)
自由落体运动的速度 v = gt,位移 s = 1/2 gt^2.
如果下落的起点与终点之间的高度差为y的话,那么所需要的时间 t = (2y/g)^0.5。
起点与终点在一条竖直线上,不需要微积分,只用简单的二次代数方程就可以算出来。
但是,如果起点和终点不在一条竖直线上,这个问题就会变得很复杂,甚至在1696年被伯努利拿来考验牛顿
这就是最速降线问题。
1,最速降线问题,
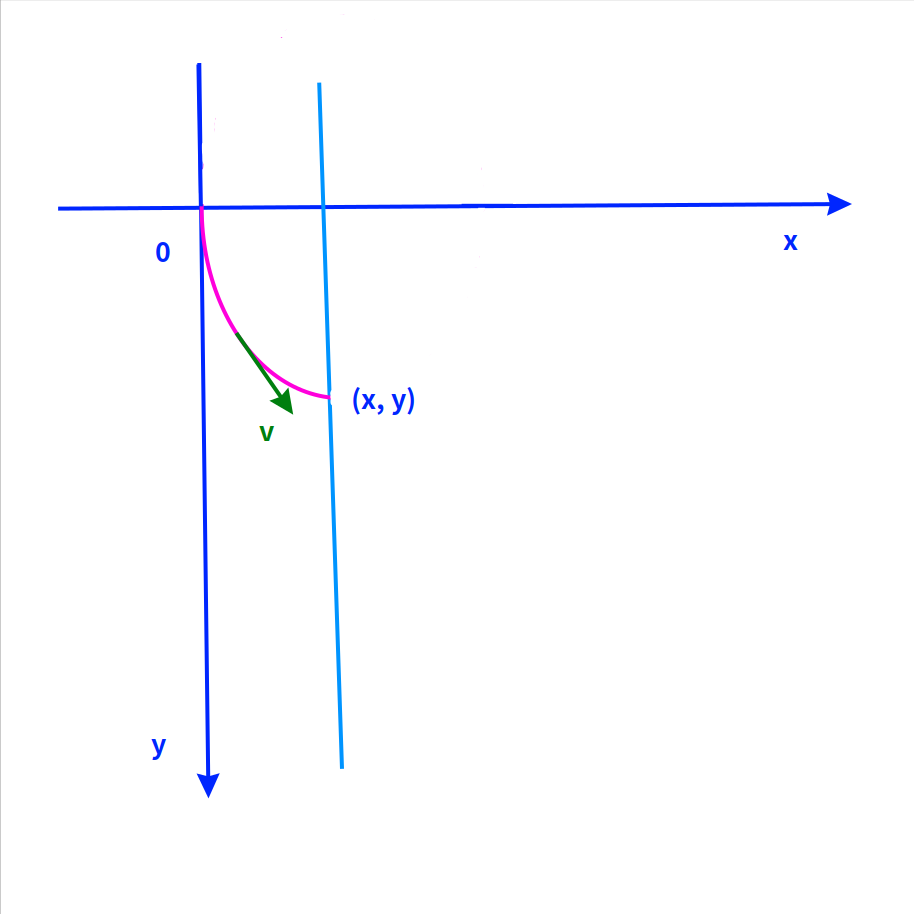
如图,不管在不在一条竖直线上,根据能量守恒定律,速度的值都是 v = (2gy)^0.5。
速率与x坐标是没关系的,因为重力做功只和高度差有关,与路径无关。
只是不在一条竖直线上时,速度的方向是变化的。
但不在一条竖直线上时,曲线的切线方向也是变化的。
并且,速度的方向始终沿着曲线的切线方向,所以它依然是个均匀加速的问题。
只是这么稍微一偏之后,就得使用微积分了:
而且,就算使用了微积分之后,问题依然不好解决。
两点之间的直线只有一条,但两点之间的曲线有无数条。
到底哪一条曲线是最节省时间的?
2,反证法、微扰论,
首先,最节省时间的曲线一定是光滑的,不可能是波纹状的。
因为,在非常微小的间隔内,速度可以认为是近似不变的,而波纹状曲线比光滑曲线具有更大的弧长。
显然,ds = vdt,波纹状的ds更大,所以肯定更费时间。
所以,最速降线的一阶导数肯定是连续变化的,而且一阶导数不能有极值点,也就是说二阶导数不能有零点。
否则,就成了波纹线了:只要把它稍微取直,花费的时间就会减少。
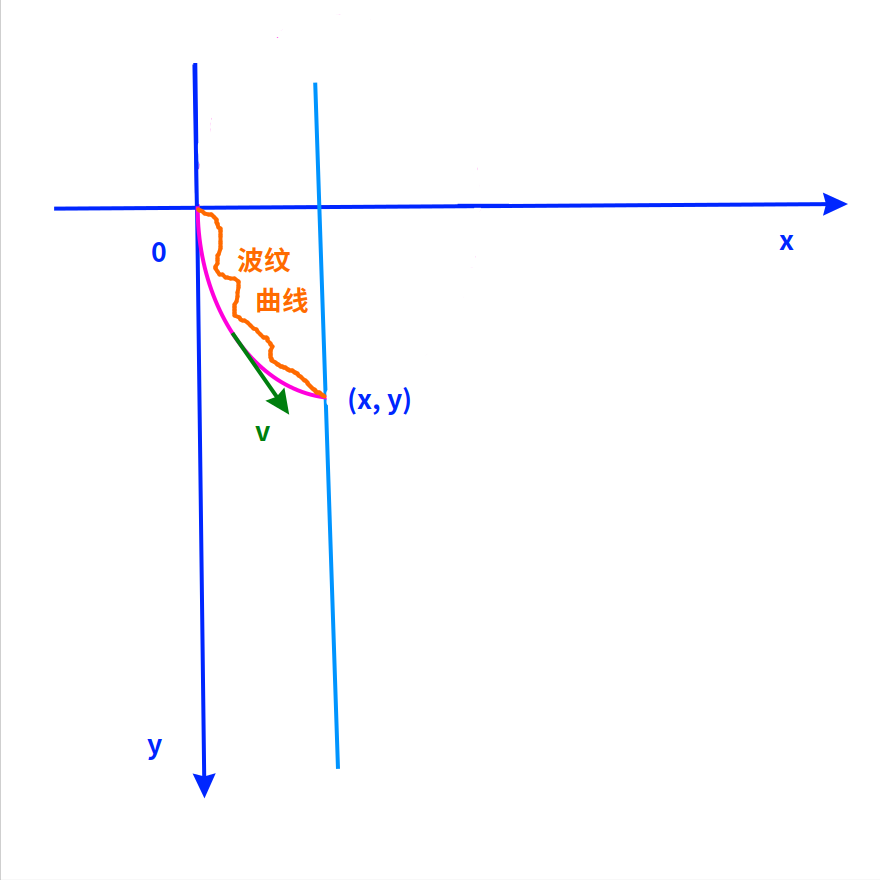
为了求出最速降线,我们假设已经求出了最速降线!
那么,只要曲线稍微有一点变动,时间就会增大。
这个方法就跟一元一次方程一样:要求某个未知数,就先设个未知数,假设它已经求出来了,然后让它直接参与运算
假设最速降线已经求出来了,任何微小的改变都会让时间增大,所以最速降线是时间的极小值:
可以把叫做y(x)的微小扰动,所以这种方法一般叫做微扰论,实际上就是反证法。
令 那么在微扰之后就变成了
时间t的改变量是微扰前后L的差对dx的积分。
在获得最优解的情况下,时间t的改变量应该为0,这种方法叫做变分法。

如果只把L按照y和y&39;的一阶导数展开,计算结果就是大名鼎鼎的欧拉-拉格朗日方程。
上图的左侧,就是欧拉-拉格朗日方程的推导过程(之前发过)。
上图的右侧,是把最速降线的公式代进去之后的结果:
如下图,化简之后,获得最速降线的微分方程 2yy&39;&39; + y&39; ^2 + 1 = 0.

解出来之后,获得x和y的参数方程,就是最速降线的解析式。
还可以进一步求出时间t的代数表达式来,如下图:

从可得
3,极限推理,
当起点-终点所在的两条竖直线极为接近的情况下:
最速降线趋近于直线,角度参数趋近于0,
正弦函数约等于角度:
(当x趋向于0时,sinx / x趋向于1)
也可以从x的参数方程看出来:
所以
也就是说:
t = (2y/g)^0.5,
y = 1/2 gt^2.
这与自由落体运动的位移时间公式是一样的。
所以,自由落体运动是最速降线的极限情况。
咸宁市召开物流供需双方座谈会 加快推进现代物流业发展
咸宁网讯记者马丽、通讯员毕璠报道:11月22日,市交通运输局联合咸宁高新区、市商务局,邀请37家制造业、商贸业、电子商务等民营企业主体,14家园区型、运输型、平台型、快递型等物流服务市场主体,召开物流供需双方座谈会。0000七月龙富贵命,八月龙九月龙一生无忧,几月出生的龙最好命
#新能源驾驶日记#七月龙的命运如同燃烧的火焰,炽热而辉煌。他们聪明机智,充满睿智和智慧,常常能够抓住机会,取得成功。他们勇敢无畏,敢于冒险,不断追求更高的目标。七月龙富贵命注定了他们拥有财富和地位,他们的生活充满了幸福和荣耀。大财经2023-12-18 11:49:500000深圳楼市,重大信号!
一线城市楼市一直是市场风向标。据国家统计局,10月份,一线城市二手住宅销售价格环比由上月上涨0.2%转为下降0.8%,其中北京、上海、广州和深圳环比分别下降1.1%、0.8%、0.8%和0.5%。0000广州医科大学 广州中山医科大学
(广州医科大学)学校简介广州医科大学简称广医,坐落于广州市,是广州市属重点高校,是一所以医学为优势和特色,开展博士、硕士、本科多层次人才培养的国家“双一流”建设高校。为教育部“卓越医生教育培养计划”试点高校、广东省高水平大学重点学科建设高校。现任党委书记唐小平,校长赵醒村。校训为“厚德修身,博学致远”。大财经2023-03-20 18:57:220000好看的官场小说 官道小说100部
大财经2023-03-22 14:10:270004




