肾脏不好的症状 肾不好的早期信号
随着近年来生活步伐的增快,人们经常面对着来自外界的各种压力,成为破坏我们身体健康的罪魁祸首。
前段时间,旧时同窗翟先生来医院找到我,因为最近的身体健康问题,让他每天都感到焦虑和压抑。据他所说,当初因家境贫寒,背井离乡在外打拼至今已三十年有余;虽说现在已成家立业,儿孙满堂,但因早期工作的特殊性,期间不乏经常出差,早出晚归,十分辛苦。

刚三十出头就被确诊为糖尿病,一开始感觉自己身强体壮,在日常饮食和用药上并没有过多注意,后来随着病情的进一步加重又被确诊为高血压,在医生的指导下服用二甲双胍、卡托普利等药物进行治疗,病情也逐渐有了好转。

但最近在一次公司聚会酒足饭饱后,发现自己小便比以往颜色明显加深,并且浮有较厚的一层泡沫,因为糖尿病症也会出现小便有泡沫的症状,加之酒过三巡,因此并未给予重视。
第二天清晨,小便异常症状只增不减,并自觉四肢乏力,恶心欲吐,双侧脚踝水肿进行性加重,意识到自己情况不妙,便紧急赶往医院就诊。
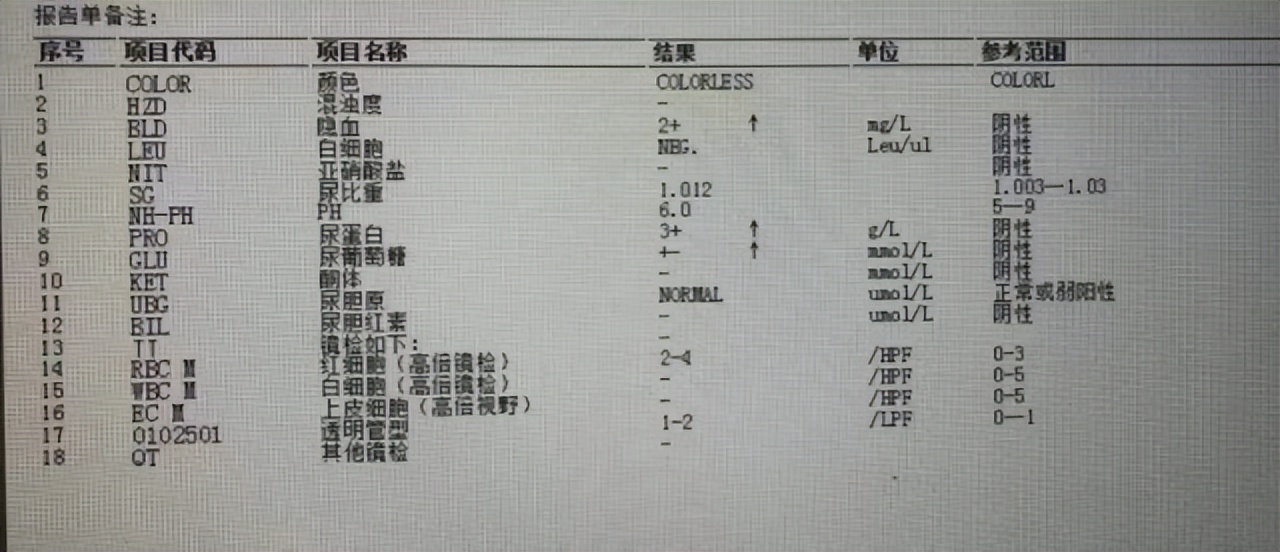
将他收入院后,经检查肾功显示:尿蛋白(+++),尿隐血(++),尿葡萄糖(+-),头颅CT显示:头颅CT平扫未见明显异常,头、颈部CT血管造影未见明显异常,结合体格检查后因糖尿病合并肾病综合征可能收入住院,给予降糖、降压、利尿、护肾等处理。
正常情况下,人体代谢废物由血液运输到肾脏,经肾脏的过滤作用形成原尿。
原尿流经肾小管时,其中的营养物质被进一步地吸收到毛细血管中,参与血液循环发挥正常的生理作用。
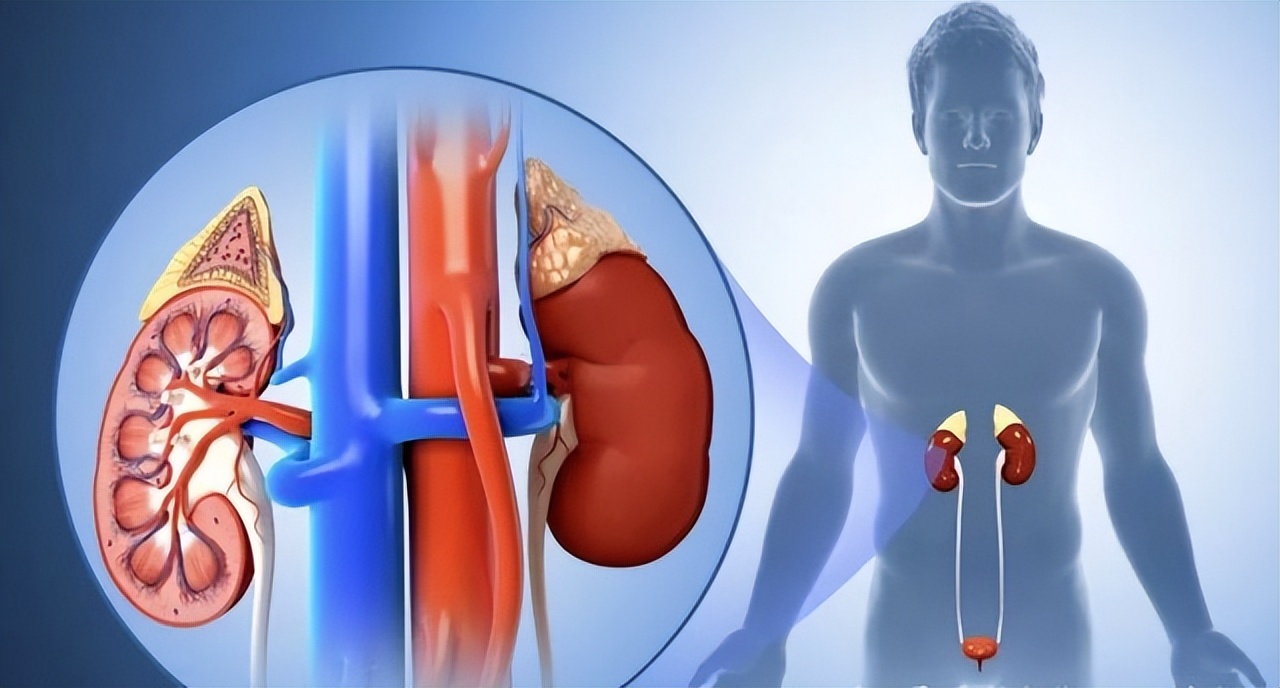
但在日常作息不规律、压力较大、抽烟酗酒或存在一些疾病的基础上,如糖尿病、高血压等。这些因素会引起肾小球硬化、肾小球系膜细胞增殖、肾小球细胞外基质增多和基底膜增厚等病理变化。
此外,该疾病还会导致患者发生肾小球滤过屏障、肾小球高灌注、高滤过状态等功能改变, 而肾小球滤过膜滤过屏障机制障碍、内跨毛细血管压力过高进而引起患者体内形成大量的微量白蛋白尿,即泡沫尿。

因此,建议有糖尿病、高血压等基础病的病人定期测定患者机体内的微量白蛋白尿水平,可将其作为反映早期糖尿病肾病严重程度的重要指标。尿液中含有蛋白时会表现为排尿时常出现有很多泡沫,这对于很多病人来说这是最直观的症状。
既然泡沫尿是肾功能损伤最典型也是最易发现的症状,那么今天我们一起聊一聊,泡沫尿到底是什么?
基于肾脏的过滤功能和对尿液的重要作用。对于很多人来说,泡沫尿的出现意味着肾脏出现了问题,事实确实如此吗?其实不然,两者既有一定的联系又有本质上的区别,泡沫尿并不等同于蛋白尿,而蛋白尿却一定会出现泡沫尿。
有学者认为,即便是正常人有时候也会出现泡沫尿,但属于正常现象,例如:
1.当日常摄水量低于机体代谢消耗量时会让尿液当中的泡沫量增加
如外出劳作,流汗较多或者在霍乱、痢疾、食物中毒的时候,由于大量津液外泄,机体极度缺乏水分,尿液颜色会变得较深且多数伴有泡沫,也会有刺鼻的氨味。
但这类的泡沫尿即便颜色较深,当摄水量增加后,会使尿液稀释,随即恢复正常。

2.与排尿时的速度和站位高低也有关系
对着小便池猛烈排尿,尤其男生站着小解时,假如站太高,在尿流的强烈冲击力下尿液非常容易激起泡沫,但这类冲击性造成的泡沫体积大、气泡量少,迅速便会裂开消退。
3.女士月经生理期
尿液中沾有经液或者男士的尿液与精液混合,尿常规也会发现蛋白尿呈现阳性,出现泡沫尿。

4.日常运动、饮食和情绪反映亦是泡沫尿产生的原因
若一次摄入大量含有蛋白质的食物或者剧烈运动、情绪波动、性兴奋后,尿道球腺分泌的黏液增多,也非常有可能会引起暂时的泡沫尿。
泡沫尿既是肾功能受损的危险因素,又是判断病情预后的关键指标。泡沫尿是肾脏结构及功能破坏的结果,也是导致肾小管间质损伤和促进肾脏病变慢性进展的关键因素。对于有基础病或肾功能异常的患者来说,定期检测尿蛋白可以更早采取措施,有利于早期诊断及制定诊疗计划。

泡沫尿是我们身体发生变化时最容易观察到的病理表现,但也意味着病情已经加重了。那么除此之外,我们日常肾系疾病的预警还有哪些呢?接下来,我们将讨论除泡沫尿之外的三种肾功能损伤早期症状。
(1)双下肢及颜面部水肿
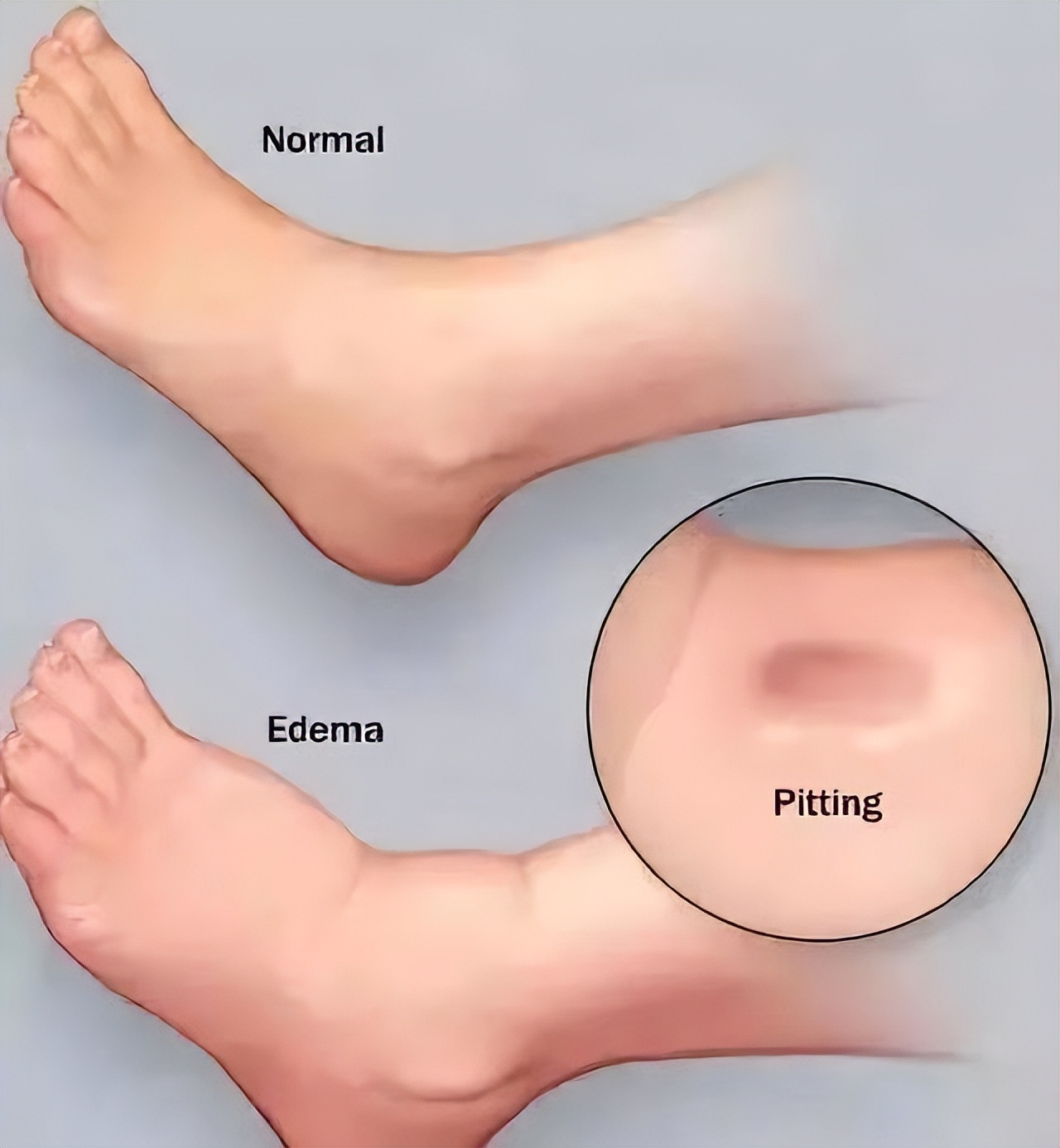
肾功能损伤患者常表现为上下眼睑或双下肢凹陷性水肿。造成水肿的病因主要是因为大量的尿蛋白潴留。肾性水肿临床以肾小球过滤明显下降为主要特征,由于肾的过滤功能减退,导致大分子蛋白质从尿液中排泄出去。
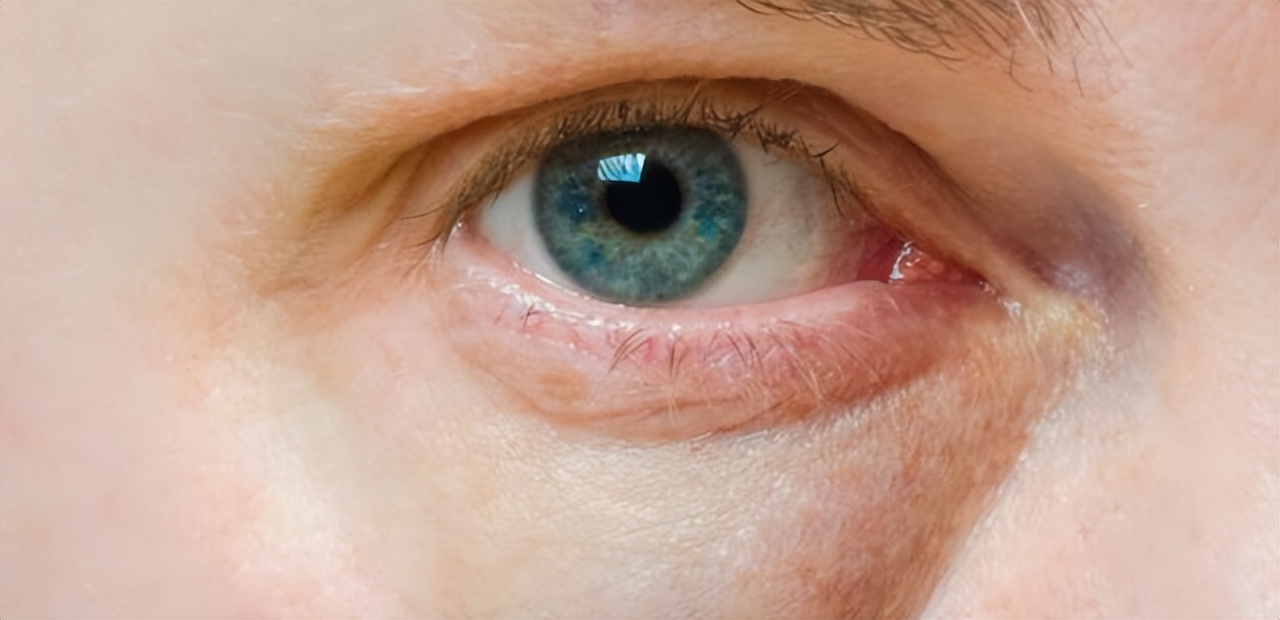
当血液中的蛋白质浓度下降,造成血浆胶体渗透压降低,血管内的液体在渗透压的作用下,渗入机体组织间隙中,造成皮下组织的水肿。除此之外,还与肾小管肾间质的钠水重吸收增强,患者毛细血管通透性增加等机制有关。
肾炎性水肿主要是与肾小球滤过率下降有关,但肾小管对钠的重吸收无相应减少。由于多种因素损害肾小球滤过膜,使得肾小球的有效滤过率减少,而肾小管对水钠的重吸收大致正常,导致水钠潴留而发生水肿。
此外,炎症因子导致毛细血管壁的通透性增加,血浆蛋白从管壁渗出,使组织液间的胶体渗透压上升,血管内的液体渗入组织间隙,进一步导致水肿。
而水肿发生时,最常出现在我们的眼睑部和下肢部,因为这些地方或肌肉组织成分少、或压力和位置较低,更易使水液停积阻滞。
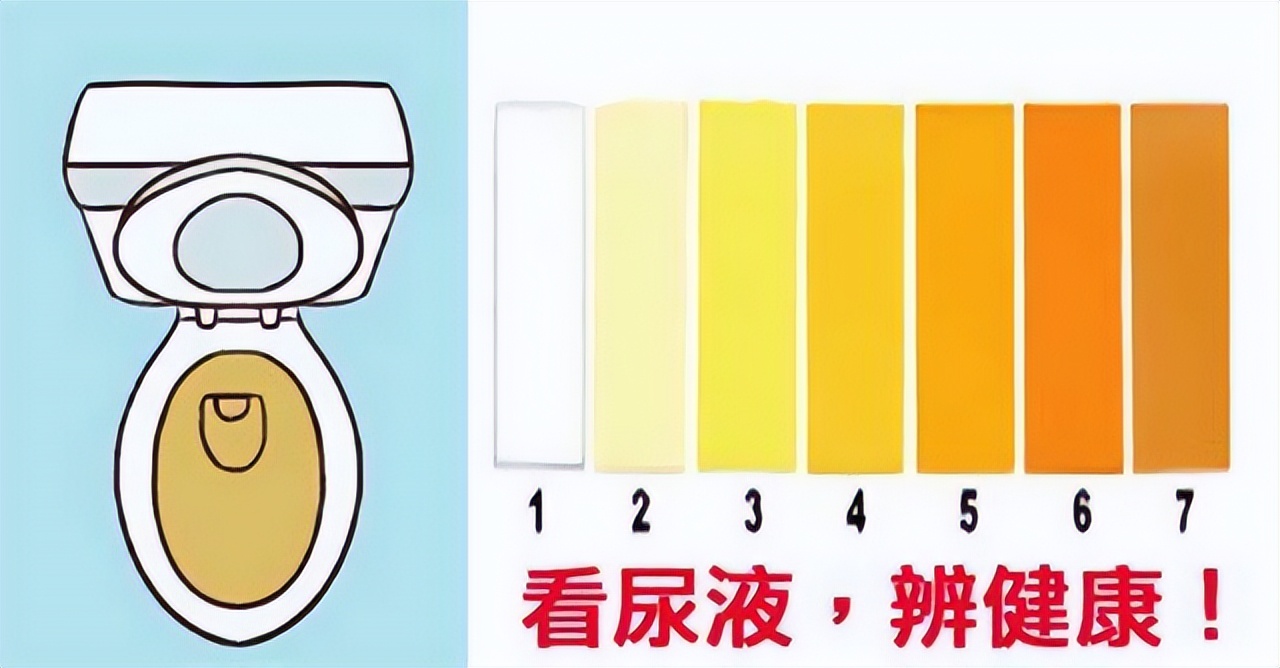
(2)尿量和颜色改变
尿液由肾脏生成,因此尿量(UV)也常常被用来作为评估肾功能的标准,其量的多少和颜色都可能预示着肾脏的健康与否。
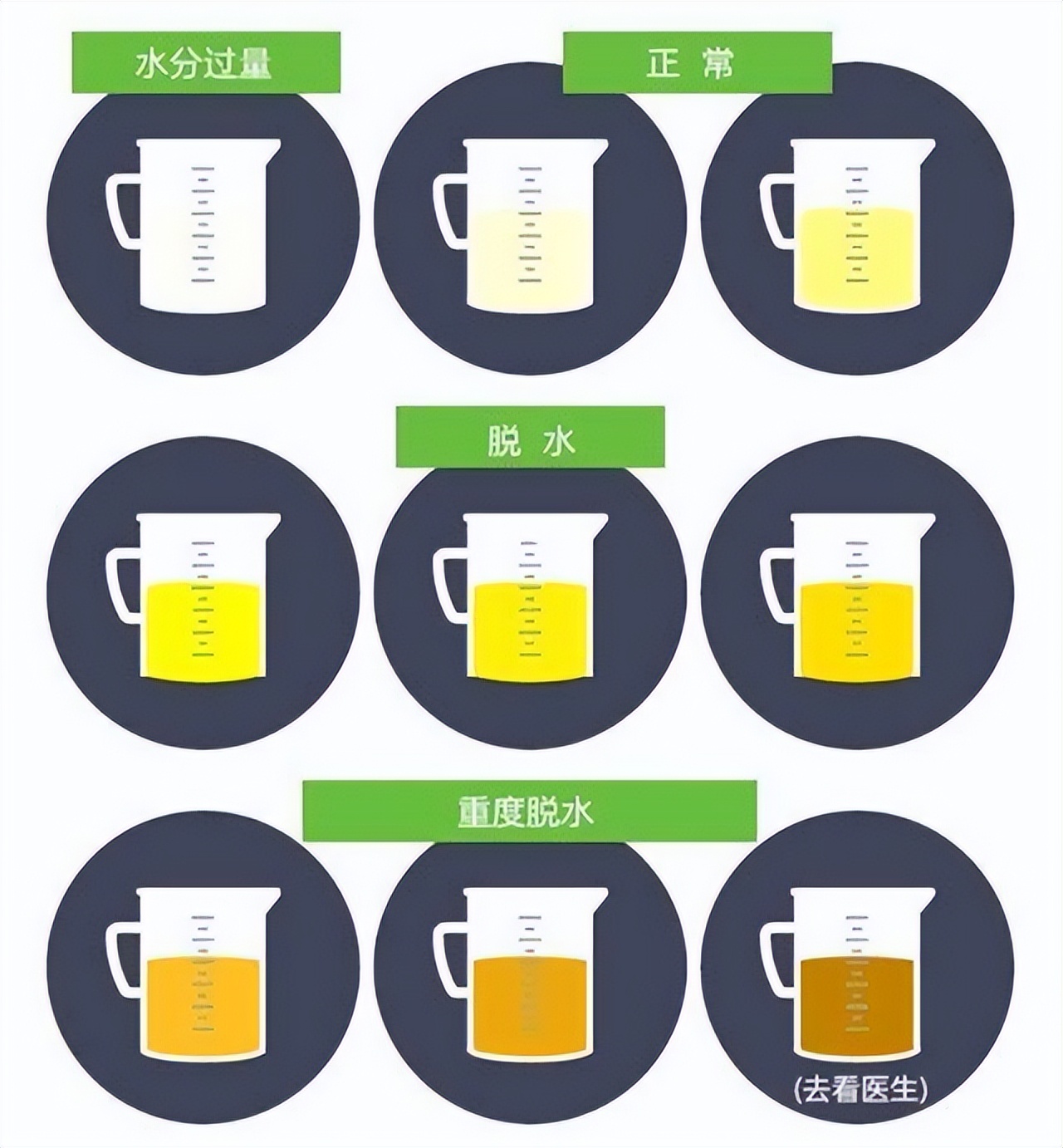
正常情况下我们人体每天排尿约1000至2000ml,呈现清澈的浅黄色或夹杂少许泡沫。肾功能是决定尿量的主要因素,但也有研究表明尿液与肾功能的改变可能并不一致。
日常饮水量过少,气候温度、劳作运动等出汗较多或者年龄较大的老年人因为肾功能减退,导致夜尿增多等生理性因素都可能导致尿量和颜色有所波动。
但长时间出现尿量改变和颜色异常也需要警惕是肾脏疾病所致,如急慢性肾炎、肾衰、尿毒症等疾病引起,发现后应尽早干预。
(3)血压升高
肾脏参与了体循环过程,对血压有着重要的调控作用,对机体血压的波动也较为敏感。在临床上肾脏病合并高血压病的案例不在少数,常有高血压肾病和肾病高血压之分,听名字二者似乎并无差别,但实则它们在形成机制和治疗措施在本质上是截然不同的。
高血压肾病,是由于长期的高血压导致肾动脉的硬化,肾小血管的硬化,从而导致肾小球的滤过率下降而导致肾功能的异常。
肾性高血压,是由于肾单侧的动脉或者双侧的动脉,他的主干以及分支变细,血流通过一个比较狭窄的管道,从而导致血压升高,引起肾功异常。
高血压所引起的肾功能异常,可表现为夜尿较以往增多,尿常规可见小管性蛋白,伴有蛋白尿(泡沫尿),或者肉眼血尿。如果不重视,得不到及时地干预治疗,可引起肾功能衰竭的发生,严重威胁患者的生命安全。
因此,如果长期高血压或出现血压比以前明显增高的症状,应定期检测肾功能,注意肾脏疾病的发生。
一旦出现机体某些部位功能改变不可掉以轻心,应尽早采取治疗措施,控制疾病的发展。
在饮食方面,建议患者选用优质低蛋白或高维生素食物为主,同时建议患者在服用一些药物或保健品时,一定要把握度不能过量,需要避免使用具有肾毒素的食物或药品。

有糖尿病、高血压、慢性肾炎等基础病的患者,在饮食方面需要注意食用低盐、低糖、低脂肪和低蛋白饮食,更要注重自身的健康护理,避免受到感染因素的影响,如食物中毒、急性胃肠炎等病症,可能会导致腹泻和呕吐,容易加重肾脏损伤。
此外,建立健康的生活方式,包括戒烟酒、增加体育锻炼,这对于人体尤其是对肾脏是有保护作用的,不仅可以增强体质,同时可以加速体内脏器的血液循环,促进肾脏排泄等,排除体内毒素,所以支持鼓励病人保证一定的日常运动。

肾功能不好的患者更应该定期复查,建议每3-6个月复查一次肾功、血尿常规。
在经过1个月的住院治疗后,好友病情已经稳定,但后续还需继续服药控制,按时复检,观测疾病进展情况。这也告诫广大朋友们,要养成健康文明的生活方式,做好自己的健康管理,做到“未病先防、既病防变”的养生原则,不仅提高机体的抗病能力,拥有健康的体魄,还能提高自己生活质量,是创建和谐美满家庭的根本要素。
参考文献:
[1]张华其,李芊.中西医结合治疗对早期糖尿病肾病尿微量白蛋白的影响[J].临床医学研究与实践,2019,4(03):126-127.
[2]衣晓峰,党元嫒.预防肾脏病 日常多留意尿液[N].中国人口报,2022-03-15(003).
[3]史永胜,邓红松,金英玉.诊断急性肾损伤标志物的研究进展[J].医学信息,2022,35(08):34-37+42.
人民币兑美元中间价突破7.1!报7.0957,较上日调升133个基点
金融界12月15日消息中国外汇交易中心显示,12月15日,人民币兑美元中间价报7.0957,较上日调升133个基点。大财经2023-12-15 10:31:150002全国各省市社会平均工资一览表(2023年10月版)!影响这些待遇!
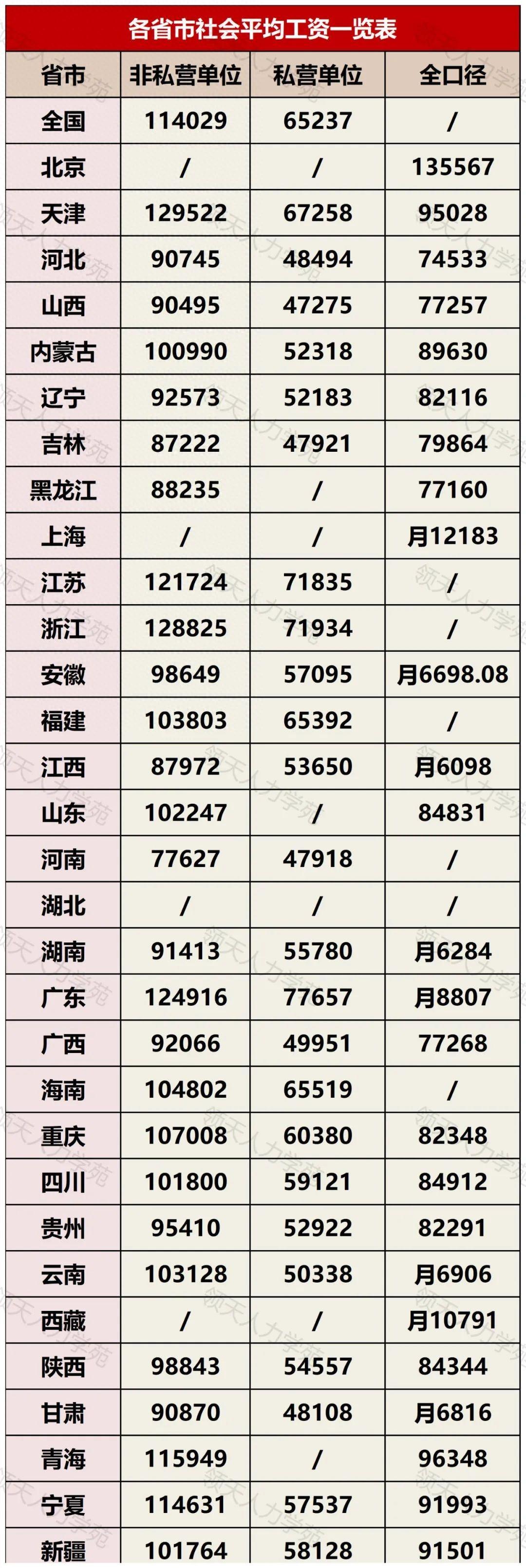
众所周知,社会平均工资是一个重要的统计数据,与企业和劳动者都密切相关。那么,社平工资会影响哪些待遇?各地的数据又是怎样的?本文为大家整理了各地社平工资一览表,以及相关问答,赶紧来看一看!01、全国各地社平工资一览表02、社平工资影响哪些待遇大财经2023-11-14 09:08:200001建信消费金融董高监名单出炉!董事长、总裁和副总裁均来自建行
界面新闻记者|曾仰琳界面新闻编辑|建信消费金融有限责任公司(下称“建信消费金融”)董高监名单出炉。6月5日,国家金融监督管理总局官网公示了《北京银保监局关于建信消费金融有限责任公司开业的批复》(下称“批复”),披露了该公司股东和持股比例,以及董事和高级管理人员名单。0000揭秘!开封的五大“穷县区”排行榜,看看有你老家吗?
众所周知,开封市是一个历史悠久的城市,但在现代经济发展的大潮中,有些县区显得相对滞后。今天,我们将为大家揭秘开封最穷的五大县区,看看这些地方究竟有哪些问题,是否也包括你的老家呢?第五名:杞县杞县虽然拥有丰富的历史文化底蕴,但在经济发展上却相对滞后。由于产业结构单一,缺乏新兴产业的支撑,加上交通不便等因素,导致经济发展缓慢,成为开封市相对较穷的县区之一。大财经2024-01-22 13:31:0500050英雄联盟怎么玩 英雄联盟幸运商店2023
说几个,我自己玩过的套路。1AD小鱼人。当时玩小鱼人,出AD,出门水晶瓶,一级点W对拼,二级学Q尝试换血。3级看好血量,如果能秒杀是最好的,杀了一次,对面上单就劣势了。那时候的鱼人机制跟现在不太一样,出AD也能打,很多人没见过AD鱼人,各种轻视,从而被我杀爆全场。出装就是三项九头蛇,最好30分钟内解决战斗,不然越到后期,AD鱼人越弱,转AP也很费劲。大财经2023-03-23 07:54:080000