omega是什么意思（听说我很穷）

好了，如果Θ你能理解了，下面四个就好理解了。

那么，常见的算法复杂度有哪些呢？

本篇文章收录于专辑：http://dwz.win/HjK，点击解锁更多数据结构与算法的知识。

前面几节讲了这么多，其实，还是只涉及了很简单的算法复杂度。

为了帮助同学们快速查阅英文资料，彤哥特地把这几节涉及到的英语单词汇总了一下：

我们先来纠正一波读音：

本节，我们就来解决这个问题。

插入排序最好的情况就是数组本身就是有序的。

o表示仅仅是大O去掉等于的情况，其他行为与大O一模一样。

关注公号主“彤哥读源码”，解锁更多源码、基础、架构知识。

本节，我们分别从读音、数学、通俗理解等三个方面阐述了Θ、O、o、Ω、ω的含义，并在最后给出了这几节涉及到的术语对应的英文，有了这些英文，你也可以快速地查阅这方面的资料。

你好，我是彤哥，一个每天爬二十六层楼还不忘读源码的硬核男人。

比如说，f(n) = 2n^2+3n+1 = Θ(n^2)，此时，g(n)就是用f(n)去掉低阶项和常数项得来的，因为肯定存在某个正数n0、c1、c2，使得 0 <= c1*n^2 <= 2n^2+3n+1 <= c2*n^2，当然，你说g(n)是2*n^2也没问题，所以，g(n)实际上满足这个条件的一组函数。

前面几节，我们一起学习了算法的复杂度如何分析，并从最坏、平均、最好以及不能使用最坏情况全方位无死角的剖析了算法的复杂度，在我们表示复杂度的时候，通常使用大O来表示。

那么，这些符号又是什么意思呢？

比如，对于插入排序，我们可以说它的时间复杂度为Ω(n)，不过，这通常没有什么意义，因为插入排序在最好的情况下很少，基本都是在最坏情况或者平均情况。

汉语英文复杂度complexity时间复杂度time complexity空间复杂度space complexity渐近分析asymptotic analysis最坏情况the worst case最好情况the best case平均情况the average case精确的渐近行为exact asymptotic behavior低阶项low order terms常数项（前置常数）leading constants松上界loose upper-bound

用函数来表示：

Ω只定义下界，只要f(n)不小于c*g(n)，就可以说 f(n)=Ω(g(n))。

用图来表示：

对于f(n)，存在正数n0、c，使得当 n>n0 时，始终存在 0 <= c*g(n) < f(n)，则我们可以用 f(n)=ω(g(n))表示。

所以，我们只需要记住大O就可以了，只不过在别人提到Θ、Ω、ω我们知道是什么含义就可以了。

ω表示仅仅是大Ω去掉等于的情况，其他行为与大Ω一模一样。

不过，我们一般说复杂度都是指的最小的上界，比如，这里插入排序的时间复杂度如果说是O(n^3)，从理论上来说，也没问题，只是不符合约定罢了。

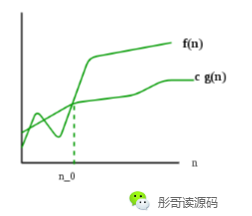
用图来表示：

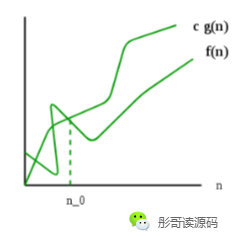
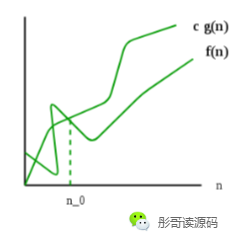
用图来表示：

对于f(n)，存在正数n0、c，使得当 n>=n0 时，始终存在 0 <= f(n) <= c*g(n)，则我们可以用 f(n)=O(g(n))表示。

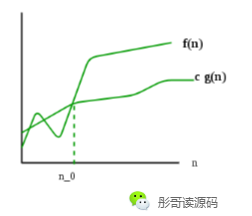
对于f(n)，存在正数n0、c1、c2，使得当 n>=n0 时，始终存在 0 <= c1*g(n) <= f(n) <= c2*g(n)，则我们可以用 f(n)=Θ(g(n))表示。

用函数来表示：

对于f(n)，存在正数n0、c，使得当 n>=n0 时，始终存在 0 <= c*g(n) <= f(n)，则我们可以用 f(n)=Ω(g(n))表示。

比如说，对于插入排序，我们说它的时间复杂度是O(n^2)，但是，如果用Θ来表示，则必须分成两条：

ωω同样定义的是下界，只不过不包含等于，是一种不精确的下界，或者称作松下界（某些书籍翻译为非紧下界）。

符号含义通俗理解Θ精确的渐近行为相当于“=”O上界相当于“<=”o松上界相当于“<”Ω下界相当于“>=”ω松下界相当于“>”

用函数来表示：

OO定义了算法的上界。

对于f(n)，存在正数n0、c，使得当 n>n0 时，始终存在 0 <= f(n) < c*g(n)，则我们可以用 f(n)=o(g(n))表示。

O，/??/，大Oho，/??/，小ohΘ，/?θi?t?/，thetaΩ，/o??meɡ?/，大Omegaω，/o??meɡ?/，小omega是不是跟老师教得不太一样^^

ΩΩ定义了算法的下界，与O正好相反。

Θ同时定义了上界和下界，f(n)位于上界和下界之间，且包含等号。

ΘΘ定义了一种精确的渐近行为（exact asymptotic behavior），怎么说呢？

用函数来表示：

不过，在我们平时与人交流的过程中，大家还是习惯于使用大O表示法，一来它表示最坏情况，最坏情况通常可以直接代表算法的复杂度，二来它比较好书写。

O只定义上界，只要f(n)不大于c*g(n)，就可以说 f(n)=O(g(n))。

用函数来表示：

但是，在其他书籍中，你可能还见过Θ、Ω、o、ω等符号。

最坏的情况下，它的时间复杂度为Θ(n^2)；最好的情况下，它的时间复杂度为Θ(n)。这里的n^2只是g(n)这一组函数中最小的上界，当然，g(n)也可以等于n^3。

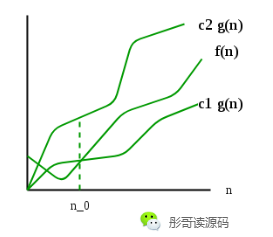
用图来表示：

用图来表示：

下一节，我们接着聊。

oo定义的也是算法的上界，不过它不包含等于，是一种不精确的上界，或者称作松上界（某些书籍翻译为非紧上界）。