谁统一了三国 谁统一三国 称什么国
如果您喜欢这篇文章,请动动发财的手指点点右上方的关注,后续我们会为您带来更多有趣的内容,方便您及时阅读,感谢您的支持。
鲁迅先生对《三国演义》中的诸葛亮的评价是“状诸葛之多智而似妖”,民间认为诸葛亮足智多谋,是古今第一的军事天才。
虽然《三国演义》将诸葛亮过于神化,但历史上真实的诸葛亮也不愧为一位伟大的政治家和军事家。
诸葛亮病亡后,就连他的竞争对手司马懿都称他为“天下奇才”,然而这样一位无所不能的天才为什么至死没能统一三国?

如果说诸葛亮神机妙算,那么另一位伟人毛泽东便可称得上是用兵如神,对于诸葛亮没能统一三国,毛主席给出了令人信服的答案。
毛泽东之所以能成为举世皆惊的政治家与军事家,和他终生手不释卷有很大关系,毛主席最喜欢读《资治通鉴》。
毛主席的护士说,他的床边总是放着一本已经泛黄并且多处用胶带修补的《资治通鉴》。
毛主席说这本书他看了17遍,对其中记载的人物诸葛亮特别感兴趣。

虽然此书带有很强的封建性质,但毛主席善于批判地继承书中的精华。
对于诸葛亮善于做思想工作、屯田的政策和他“鞠躬尽瘁、死而后已”的精神,毛主席大为赞赏,并学习诸葛亮的智慧,对实际工作进行有效指导。
诸葛亮曾经对年老的黄忠采用激将法,使他最终打败了夏候渊,毛主席将诸葛亮的这一做法用于前线的宣传工作。
井岗山时期部队的成员来自不同地方,没有统一思想,毛主席告诉红军指战员要学习诸葛亮,把思想工作做好。

最后,还不忘对战士加以肯定,说我们的战士思想觉悟很高,很快就能转过弯儿来。
在所有人的共同努力下 ,最终成长为一支有着坚定信仰、并且能打硬仗胜仗的部队,这也为共产党能取得革命的最后胜利奠定了坚实的思想基础。
没有统一的思想和坚定的信仰,革命不可能取得最终的胜利,毛主席在这方面可以说把诸葛亮的“激将法”结合时代的背景运用到了极致。
毛主席对诸葛亮屯田的政策也是赞誉有加,1955年面对如何安置大量的部队退役人员时,毛主席对参与讨论的王震将军说:“可以组织屯垦戊边嘛,中国古代就有屯恳制,管仲搞过, 诸葛亮在汉中也搞过呢,开荒就业,治疗战争创伤,巩固边疆,应该是个好办法。”
毛主席经常要求大家要学习诸葛亮精神,充分发挥人的主动性,又快又好地建设我们的新中国。

毛主席最为欣赏诸葛亮的是他“鞠躬尽瘁,死而后已”的精神,青年求学时期的毛主席把前后《出师表》背得滚瓜烂熟。他说:“读诸葛亮《出师表》而不流泪者,其人必不忠”。
毛主席曾多次提倡我党干部要学习诸葛亮“鞠躬尽瘁,死而后已”的精神,并表示:“我也要鞠躬尽瘁,死而后已呢”!
如果说诸葛亮之所以被后世人铭记是因为他“鞠躬尽瘁,死而后已”的精神,那么毛主席就成为中国人民的领袖,成为世界近现史上最伟大的人物之一就是因为他的永远“为人民服务”的信仰。
毛主席也从诸葛亮身上的错误受到启发,为我军找到了一条发展之路,使我军每战必胜。
那么毛主席从诸葛亮身上找出的三个错误是什么,毛主席又从中得到了什么样的启示?

1957年,毛主席在一次讲话中说:“中国有一句俗语:‘三个臭皮匠,顶一个诸葛亮’,但单独的诸葛亮也不是完美的,存在一些缺陷”
毛主席认为诸葛亮的缺陷主要体现在他有三个失误。
刘备三顾茅庐之后,诸葛亮出山,《隆中对》为刘备制定了平定天下的作战方针,指出他要完成统一大业,必须先夺取荆州、益州,然后以这两地为据点,辐射周边,继而夺取中原。
《隆中对》历来为世人所推崇,认为诸葛亮对天下局势的分析很到位,为刘备恢复汉室的未来战略也很精彩。

而毛主席却认为,这一战略存在着根本问题,是蜀汉最后灭亡的根本原因。毛主席为什么这么说?
1959年,毛主席在中央会议上说:“人的认识是逐步发展,不可能如同诸葛亮那样,事先安排锦囊妙计,千里之遥而二分兵力,其终则关羽刘备诸葛三分兵力,安得不败”。
毛主席认为,在《隆中对》的作战方针下,刘备虽轻松拿下了荆州、益州二地,建立了蜀国,但他们三分兵力,进行战争的战略是错误的。
所谓三分兵力,指的是让关羽父子驻守荆州,最后其命丧孙权之手;刘备为给关羽报仇,不顾群臣反对,又领一部分兵,东伐东吴,最后命丧白帝城;刘备死后,诸葛亮又带领下的兵力,北伐曹魏, 最后大败。
毛主席是一位伟大的军事家,他认为三分兵力必然会导致失败,应该集中优势兵力一举出击制敌。毕竟蜀国当时的实力最为弱小,只有集中兵力才能发挥最大价值。

且荆州与益州相距甚远,当时蜀汉的军队并不多,荆州刚被占领,诸葛亮便想拿下益州。
在攻益州的同时攻打荆州,益州的兵将很难迅速赶来救援。再加上关羽一时大意和轻敌,孙权趁虚而入,蜀国荆州失去了荆州这块战略要地,关羽还被杀了。
荆州失守,就是因为刘备的援军太远了,他们只能眼睁睁看着孙权攻陷荆州。关羽的死激起了刘备报仇之心,但他操之过急,最终死在白帝城。
从这个时候开始,蜀汉的军事实力开始衰退,最终导致无法完成统一大业。
在毛主席看来,诸葛亮的策略存在不足,他太急功近利,应该拿下荆州之后,休整军队。
等自身实力足够强大了,再出兵益州,进而一步步完成匡扶汉室的大业。
毛主席受此启发,提出农村包围城市,武装夺取政权的创新性伟大决策。

当时我党的红军和蒋介石的国民党军队实力相差悬殊,因此毛主席根据实际情况,避开敌人统治力量薄弱的城市,发展农民为革命主体,将红军与农民合二为一,让处于劣势地位的我党焕发出勃勃生机。
解放战争时期,毛主席将这一战略进一步发展到了极致。战争初期,国民党军队无论从武器装备,还是人数上都远远超过解放军。
因此,毛主席提出:初期应该是战略防御的舞台,用战争来养战争,使解放军队伍不断扩大。
果不其然,面对国民党的攻势,解放军通过一个个小战役,不断消耗国民党的兵力,而解放军却在后方不断发展自身的实力。

一直到解放战争后期,解放军与国民党军队在人数方面已经相差无几了,随后,毛主席一声令下,三大战役打响,解放战争进入战略反攻阶段,最终,中国人民获得了解放战争的胜利。
毛主席就是这样不在意一城一池的得失,从大局出发,在保护好革命根据地的同时发展实力,在时机成熟时发起反攻,最终率领人民获得了解放战争的胜利。
诸葛亮犯的第二个错误是用错了人,这主要指的是错用了关羽和马谡二人。前者大意失了荆州,后者自负失了街亭。
诸葛亮受命前去四川时,让关羽留守荆州,而这一决定使得关羽不仅失掉了荆州,自己也被东吴所杀。

毛主席认为让关羽守荆州是错误的,因为关羽为人骄傲,不肯实行诸葛亮联吴拒魏的计谋。
《三国志》作者陈寿说他“刚而自矜”,毛泽东认为关羽这个人并不高明,对待同盟军搞关门主义,致使蜀汉失去了荆州。
而荆州对蜀国来说是非常重要的战略之地,失了荆州,导致蜀国遭受到毁灭性的打击。
邓小平很少评说历史,但他却对诸葛亮任用关羽的态度作了这样的评价:诸葛亮用人讲手段,但对关羽就非常迁就甚至不讲原则,助长了关羽的骄傲情绪,故后来铸造成大错。
毛主席吸取了关羽的教训,一直注重对内对外的合作,对内毛主席团结农民,在农村建立良好的群众基础,注重工农联合;对外毛主席在抗日战争时放下两党恩怨,同国民党一致对抗日本侵略者。
其实,诸葛亮在第二次北伐时有机会取得成功,但因为误用一人导致整个北伐的失败,这个人就是马谡。

马谡虽是个不可多得的人才,他却有一个缺点—太过于刚愎自负。
诸葛亮一再强调街亭的重要性,此地关乎着整个北伐的战局,并且告诉他一定要在有水源的地方安营扎寨,士兵应该24小时不间断巡逻,时刻保持警惕,防止敌军偷袭。
可是马谡到达街亭之后完全将诸葛亮的命令抛在脑后,甚至认为诸葛亮太过谨慎,魏军绝对没有他想象的那么厉害。于是他自作主张,将守军部署在远离水源的街亭山上。
魏军看后立刻将街亭的水源切断,还将所有能运输物资的道路全部掐断,然后放火烧山。没有了粮草与水源的补给,马谡不战而败。
面对街亭失守,诸葛亮挥泪斩了马谡。毛主席认为北伐的失利不是马谡失了街亭,主要是诸葛亮用人的失误。
马谡是一个十分骄傲自大的人,虽然他精通兵法,平时提意见和战术还可以,让他率兵打仗,以他的性格不可能不败。
可是诸葛亮却认为马谡性格上的缺陷可以改正,导致街亭失守北伐失利,蜀国再无强盛的可能。

清末文学家毛宗岗评价说:诸葛亮失街亭后几无退出,不得不弃三城,用空城计退追兵。而之前的擒夏侯、斩崔谅、杀杨陵、骂王朗、破曹真等这些事情都统统白做。
那么,诸葛亮为什么要用这两个不该用的人?他的用人原则是什么?
诸葛亮用人严格按照他的“七观法”,所谓“七观法”就是:问之以是非而观其志;穷之以辞辩而观其变;咨之以计谋而观其识;告之以祸难观其勇;醉之以酒而观其性;临之以利而观其廉;期之以事而观其信。
在所有人的要求下,诸葛亮最在乎的是道德品质。如果这个人在道德品质上有些许问题,那他不会选用,直接导致了蜀汉后期的“人才危机”。
毛主席认为这种识人方法好是好,但不适合那样的乱世,而曹操的“唯才是举”倒要高明得多。

“金无足赤,人无完人”,天下虽大,找一个诸葛亮已经很不易,别说满朝文武都是“诸葛亮式”的人才了。
新中国成立初期,很多解放军将领都是农民出身,几乎没上过学。然而,毛主席根据自己的方法,让这些将领们充分发挥了聪明才智,使他们在一场场战斗中取得了胜利。
特别是在抗日军政大学的建立,它解决了战场上许多军队指挥官的错误,毛主席的高瞻远瞩让诸葛亮的悲剧并没有发生在解放军身上。
如果说诸葛亮以上的两个错误没有规避,但他能在第一次北伐时亲自指挥军队的话,也许事情还会有一线转机。
可诸葛亮偏偏没有坐阵军中,致使马谡丢了街亭并被斩,毛主席说这就是诸葛亮的第三个错误。
对于马谡失街亭一事,诸葛亮认为他没有亲自指挥军队是导致街亭失守的根本原因。他在“资治通鉴.卷七十一魏纪三》街亭之战的段落旁,做了“初战,亮宜自亲临”的批注。

把军队分散,责任交给别人,必然会导致无法及时掌控整个战局,而在马谡被曹魏大军围困时,也没有及时出兵支援和策应,街亭沦陷,后面的战事接连失利,北伐以失败告终。
作为三军主师,不仅要对整场战争有谋略、有策划,更要结合战场的实际情况进行分析。综合考虑,选择有利时机进攻,对战场突发情况亦应有合理预案。
事实证明,毛主席对这一错误的指出完全正确。因为后来,诸葛亮出师木门道杀张郃事,说明诸葛亮意识到了此前的错误。毛泽东因此批注:“每出,亮必在军。”
如果诸葛亮能早一点意识到此问题,马谡也不会“含冤”被斩,可惜历史不能重来。

毛主席在读了这段历史之后,充分认识到了主帅亲临战场的重要性。
在后来的革命战争中,很好地规避了这种错误。
解放战争时期,毛主席和其他解放军部队的指挥员,打仗时几乎总是站在最前线,他们通过电报总结每个战场的详细信息,再与每个负责指挥的人员讨论,确定最佳的作战方案,获取了战斗的彻底胜利。
虽然毛主席指出了诸葛亮的三个错误,但毛主席对诸葛亮的评价其实是很高的,毛主席的伟大之处就在于他能批判地继承古人的经验智慧,然后用它来指导我们的军队取得最后的胜利。
那么,毛主席从诸葛亮身上学到了什么?
毛主席对诸葛亮在兵器方面的改革特别赞赏。他在1962年与南京炮兵工程技术学院的院长孔从洲谈日新月异的科学技术时,谈到了诸葛亮对兵器的创新和改进。

说诸葛亮把我们之前使用的一次只能发射两三只箭的弩机,做了改良,使弩机可以一次连续发射十支箭,并大大提高了弩机射箭的准确性,在征孟获时便使用这种武器。
没想到孟获也找到了对敌的办法,他的三千藤甲军让诸葛亮的弩机彻底失去了作用。
哪知诸葛亮技高一筹,研究了孟获得藤甲后发现,是用油浸过的,于是一把火把藤甲军烧了。
诸葛亮发明的这种弩被后人称为“诸葛连弩”,据载,诸葛连弩是世界上最早的自动武器。
他的聪明才智和改革创新能力即使在今天也十分难得,这也是毛主席对诸葛亮赞叹有加的原因之一。
诸葛亮对孟获的“七擒七纵”能很好地处理民族矛盾,他这种处理民族关系的做法是毛主席最为推崇的。

在毛主席的指示下,刘伯承妥善处理了和彝族首领结盟的事。毛主席对他的做法大加赞赏,夸他比诸葛亮还厉害。
1953年,面对擒获的布依族女首领该不该杀的问题时,毛泽东对当时汇报这件事的西南军区参谋长李达说:“不能杀,你们做得很好,好不容易出了一个女匪首,正好又是少数民族,这是一个非常好的机会,你们不妨学习一下诸葛亮如何擒孟获,他“七擒七纵”,你们就不能“八擒八纵”吗?一擒就杀的做法不可取。”
当时被擒的女首领叫程莲珍,她和当地的很多少数民族都奉行落后的奴隶制度,毛主席要求帮助这些地区废除奴隶制,进行民主化改革。

程莲珍和很多部落的首领为了阻碍解放军废除奴隶制,带着部落的人举兵叛乱,结果没几个回合就被解放军活捉了。
一些首领认识到时代的大势所趋,乖乖投降,听从解放军的安排。但个别顽固派表面顺从,暗里继续抵抗。
军区参谋长李达在请示了毛主席后,采用了毛主席教导的“七擒七纵”的办法,慢慢地引导这些少数民族的将领和士兵。

曾经被生擒又被放走的程莲珍最终转变了思想,回到匪穴,告诉曾经的“兄弟”共产党的政策如何好,自己如何受到优待。
程莲珍的现状使土匪兄弟们看到了希望,如果不是旧社会生活所迫,谁愿意上山当土匪呢,他们纷纷下山投降,过上了稳定的生活。
那些顽固抵抗的少数民族首领手下的士兵也渐渐明白,他们打不赢解放军,而且冲在前面死伤的还是最底层的百姓。
最终,解放军的真诚和良苦用心打动了他们,奴隶制被彻底肃清,直到现在,西南地区都保持着和平与安定。
毛主席善于学习历史,善于古为今用,因此解决了很多革命和建设中的问题,也因此成为世界上最有智慧,最伟大的领袖之一。
毛泽东与诸葛亮同为中国历史上家喻户晓的名人、他们在长达1700多年的时间轴上各自闪耀着自己独特的光芒。

诸葛亮一生为辅佐刘备匡扶汉室“鞠躬尽瘁,死而后已”,毛泽东一生为党为人民奉献自己的全部身心;
诸葛亮一生用人唯“七观法”是瞻,毛泽东一生知人善任,不拘一格;
诸葛亮一生事必亲躬,关键时刻却没有在重要的战场亲自指挥,毛主席善于团结干部,对战场上的信息汇总跟每位领导讨论最佳作战方案;
他们都曾身处乱世,都曾力挽狂澜,诸葛亮“出师未捷身先死”,毛主席成就新中国伟业,他们的精神必将成为后世人学习的楷模,他们的智慧也必将带给后来的人们无限的启示。
“以铜为镜,可以正衣冠,以古为镜,可以知兴替”。
今天的我们,从历史中学会了很多,明天的我们,必将用增长的智慧去开创更为美好的生活。
太上头!在番禺“挖呀挖呀挖”,能挖出哪些“宝藏”呢?
“在小小的花园里面,挖呀挖呀挖,种小小的种子,开小小的花”这魔性的旋律,让不少人大呼“好上头”!那放眼番禺,都能“挖”到什么呢?今天,就带你一起,搭配最火的节奏,打起节拍,在番禺一起挖~准备好了吗?来咯~♫♫大财经2023-05-20 18:40:340000地表水环境质量标准 环境标准查询官网
为支撑相关生态环境质量标准、风险管控标准和污染物排放标准实施,近期,生态环境部发布《水质6种邻苯二甲酸酯类化合物的测定液相色谱-三重四极杆质谱法》(HJ1242-2022)、《土壤和沉积物20种多溴联苯的测定气相色谱-高分辨质谱法》(HJ1243-2022)和《地表水环境质量监测技术规范》(HJ91.2-2022)3项国家生态环境标准。0001先进制造业强市淄博行丨遨博机器人:做行业标准的制定者与推动者
记者张文珂5月24日—26日,为期三天的擎起“新齐帜”——“先进制造业强市淄博行”大型全媒体采访活动启动,淄博市委网信办组织中央、省、市25家新闻媒体走进淄博先进制造企业,通过深入采访,小切口、多视角、深挖掘,生动展现淄博百年老工业城市迈向先进制造业强市的奋进历程。5月25日上午,齐鲁晚报·齐鲁壹点跟随采访团走进本次活动的第五站——遨博(山东)智能机器人有限公司。大财经2023-05-27 11:51:160000盘前必读丨独董制度重大改革下月实施;年内最大IPO华虹公司今日上市
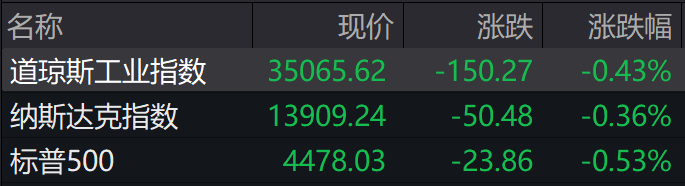
【财经日历】华虹公司在科创板上市上证科创板100指数正式发布当地时间上周五,美国三大股指冲高回落,最终全线收跌。截至收盘,道指跌0.43%,纳指跌0.36%,标普500指数跌0.53%。道指一周累计下跌1.11%,纳指下跌2.85%,标普500指数下跌2.27%。大财经2023-08-07 10:01:180000橡木家具好不好 橡木实木家具怎么样
说到家庭具很多会选择实木家庭具,觉得耐用,实用,方便,刚好橡木又是实木家庭具的其中一种,一种不错的家庭具选择之一,看起高端,大气,上档次,这里小编就跟大家庭一起说说橡木家庭具最好吗?如何选购橡木家庭具?看是不是橡木家庭具真的有那么的最好。橡木家庭具最好吗?大财经2023-03-25 13:38:040000